| 坐标方法的简单应用 |
主编:黄冈中学数学集体备课组
一、知识归纳
1、利用平面直角坐标系绘制区域内一些地点分布情况平面图的过程如下:
(1)建立坐标系,选择一个适当的参照点为原点,确定x轴、y轴的正方向;
(2)根据具体问题确定单位长度;
(3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称.
2、在平面直角坐标系中,将(x,y)向左(或右)平移a个单位长度,可以得到对应点(x-a,y)(或(x+a,y ));将点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x,y+b)(或(x,y-b)).
二、例题讲解
例1、(1)如图,若在象棋盘上建立直角坐标系,使“将”位于点(1,-2),“象”位于点(3,-2),则“炮”位于点( )
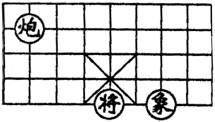
A.(1,3) B.(-2,1)
C.(-1,2) D.(-2,2)
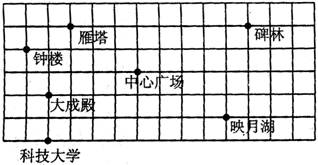
(2)如图所示是某市旅游景点的示意图,试建立平面直角坐标系,用坐标表示各个景点的位置.
(3)如图,四艘船M、N、P、Q与灯塔O的距离均为50海里,则在灯塔O西偏南70°且与O相距50海里的船是( )
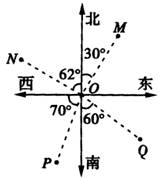
A.船M B.船N C.船P D.船Q
答案:
(1)B
(2)答案不唯一
以科技大学所在水平直线为横轴,钟楼所在竖直直线为纵轴建立坐标系,科技大学(1,0),钟楼(0,4),大成殿(1,2),雁塔(2,5),中心广场(5,3),碑林(10,5),映月湖(9,1).
(3)C
例2、(1)若把P(3,-1)沿y轴正方向平移2个单位,再沿x轴负方向平移6个单位得到点P′,则P′的坐标为( )
A.(-3,2) B.(9,1)
C.(-3,1) D.(3,-1)
(2)在平面直角坐标系中,△ABC的各顶点的坐标分别为A(-3,2),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P1(a+6,b+2),则平移后的△A1B1C1的各顶点坐标分别为A1( ),B1( ),C1( ).
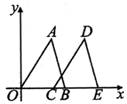
(3)如图所示,△OAB的顶点B的坐标为(4,0),把△OAB沿x轴向右平移得到△CDE,如果CB=1,那么OE的长为__________.
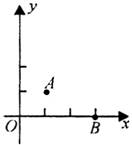
(4)如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )
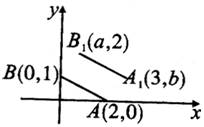
A.2 B.3 C.4 D.5
(5)如图,在平面直角坐标系中,以O(0,0),A(1,1),B(3,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
A.(-3,1) B.(4,1)
C.(-2,1) D.(2,-1)
答案:
(1)C (2)A1(3,4),B1(1,3),C1(4,2)
(3)7 (4)A (5)A
例3、张老师住在学校的正东200米处,从张老师家出发向北走150米就到李老师家,若选取李老师家为原点,分别以正东、正北方向为x轴、y轴正方向建立平面直角坐标系,则学校的坐标是( )
A.(-200,-150) B.(200,150)
C.(-150,-200) D.(150,200)
答案:A
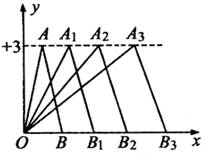
例4、如图所示,在直角坐标系中,第一次将△AOB交换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).
(1)观察每次变换前后的三角形有何变化,找出规律,按此规律再将△OA3B3变换成△OA4B4,则A4的坐标是___________,B4的坐标是____________.
(2)若按(1)中找出的规律,将△OAB进行n次变换,得到△OAnBn,则An的坐标是___________,Bn的坐标是____________.
答案:
(1)(16,3),(32,0)
(2)(2n,3),(2n+1,0)
高一全科点睛班课程 高一全科强化班课程 高二全科全年强化班 高三全科强化班课程 初一全科强化班课程 初一全科点睛班课程 初二全科强化班视频 初二全科点睛班课程 初三全科强化班 全科巨无霸同步提高课程 小学全年全科强化班
- 返回 -