例、将长度为2n(n为自然数,且n≥4)的一根铁丝折成各边的长均为整数的三角形,记(a,b,c)为三边的长,且满足a≤b≤c的一个三角形.
(1)就n=4,5,6的情况,分别写出所有满足题意的(a,b,c);
(2)有人根据(1)中的结论,便猜想:当铁丝的长度为2n(n为自然数且n ≥4)时,对应(a,b,c)的个数一定是n-3,事实上,这是一个不正确的猜想;请写出n=12时的所有(a,b,c),并回答(a,b,c)的个数;
(3)试将n=12时所有满足题意的(a,b,c),按照至少两种不同的标准进行分类.
解:
(1)当n=4时,铁丝长度为8,满足题意的(a,b,c)只有一组:(2,3,3);
当n=5时,铁丝长度为10,满足题意的(a,b,c)有两组:(2,4,4),(3,3,4);
当n=6时,铁丝长度为12,满足题意的(a,b,c)有三组:(2,5,5),(3,4,4),(4,4,4).
(2)当n=12时,铁丝长度为24,则a+b+c=24,且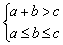 ,
,
由此得8≤c ≤11,即c=8,9,10,11,
故满足题意的(a,b,c)共有12组:
(2,11,11),(3,10,11),(4,9,11),(5,8,11),
(6,7,11), (4,10,10),(5,9,10),(6,8,10),
(7,7,10), (6,9,9), (7,8,9), (8,8,8).
(3)不同的分类标准,决定不同的分类,现举例如下:
①按最大边c的值分类,有四类;
②根据是否等边、等腰三角形分类,共有三类;
③根据最大角与直角的关系分类,共有三类.