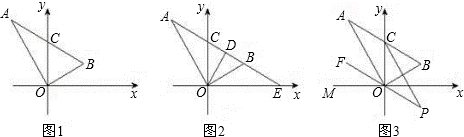
例、如图1，在平面直角坐标系中，△AOB是直角三角形，∠AOB＝90°，斜边AB与y轴交于点C．
（1）若∠A＝∠AOC，求证：∠B＝∠BOC；
（2）如图2，延长AB交x轴于点E，过O作OD⊥AB，若∠DOB＝∠EOB，∠A＝∠E，求∠A的度数；
（3）如图3，OF平分∠AOM，∠BCO的平分线交FO的延长线于点P，∠A＝40°，当△ABO绕O点旋转时（斜边AB与y轴正半轴始终相交于点C），问∠P的度数是否发生改变？若不变，求其度数；若改变，请说明理由．
分析：
（1）由直角三角形两锐角互余及等角的余角相等即可证明；
（2）由直角三角形两锐角互余、等量代换求得∠DOB＝∠EOB＝∠OAE＝∠E；然后根据外角定理知∠DOB＋∠EOB＋∠OEA＝90°；从而求得∠DOB＝30°，即∠A＝30°；
（3）先求得△ABO旋转前的度数∠P＝25°；然后由角平分线的性质知∠FOM＝45°－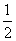
∠AOC ①，∠PCO＝
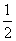∠A＋
∠A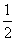OC ②，根据①②解得∠PCO＋∠FOM＝45°＋
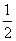∠A，最后根据三角形内角和定理求得旋转后的∠P的度数．
解：（1）∵△AOB是直角三角形，
∴∠A＋∠B＝90°，∠AOC＋∠BOC＝90°，
∵∠A＝∠AOC，
∴∠B＝∠BOC；
（2）∵∠A＋∠ABO＝90°，∠DOB＋∠ABO＝90°，
∴∠A＝∠DOB，
又∵∠DOB＝∠EOB，∠A＝∠E，
∴∠DOB＝∠EOB＝∠OAE＝∠OEA，
∵∠DOB＋∠EOB＋∠OEA＝90°，
∴∠A＝30°；
（3）∠P的度数不变，∠P＝25°．理由如下：
∵∠AOM＝90°－∠AOC，∠BCO＝∠A＋∠AOC，
又OF平分∠AOM，CP平分∠BCO，
∴∠FOM＝45°－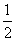
∠AOC ①，∠PCO＝
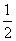∠A＋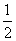
∠AOC ②，
①＋②得：∠PCO＋∠FOM＝45°＋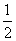
∠A，
∴∠P＝180°－（∠PCO＋∠FOM＋90°）
＝180°－（45°＋
∠A＋90°）＝25°．
点评：
本题综合考查了三角形内角和定理、坐标与图形的性质．解答时，需注意，△ABO旋转后的形状与大小均无变化．
