例、(“希望杯”试题)如图,对于任意五角形ABCDE,求∠A+∠B+∠C+∠D+∠E的度数.
解法一:如图,在△AMN中,∠A+∠1+∠2=180°.
∵∠1,∠2分别是△CEM和△BDN的外角,
∴∠1=∠C+∠E,∠2=∠B+∠D.
∴∠A+∠B+∠C+∠D+∠E=∠A+∠1+∠2=180°.
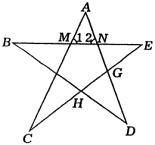
解法二:如图,在△ACG中,∠A+∠C+∠AGH=180°.
∵∠AGH,∠GHD分别是△HGD和△BEH的外角,
∴∠AGH=∠D+∠GHD,∠GHD=∠B+∠E.
∴∠A+∠B+∠C+∠D+∠E=∠A+∠C+∠GHD+∠D
=∠A+∠C+∠AGC=180°.
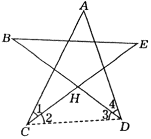
解法三:如图,连结CD,则
在△ACD中,∠A+∠1+∠2+∠3+∠4=180°.
又∠BHE=∠CHD,
∴∠2+∠3=∠B+∠E.
∴∠A+∠B+∠C+∠D+∠E=∠A+∠2+∠3+∠1+∠4=180°
剖析:
本题主要运用了三角形内角和定理及外角的有关结论,把所求的五个角集中到一个三角形中来解决.这是化归思想的又一体现,同学们应细心领会并加以掌握.