| 多边形及其内角和 |
主编:黄冈中学数学集体备课组
一、知识归纳
1、多边形:在同一平面内,由一些线段首尾顺次相接组成的图形叫做多边形.
如果一个多边形由n条线段组成,那么这个多边形叫做n边形.
2、正多边形:各边相等,各角也相等的多边形叫做正多边形.
3、n边形的内角和等于(n-2)·180°.多边形的外角和等于360°.
4、对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
从n边形的一个顶点出发有(n-3)条对角线,n边形共有
条对角线.
二、例题讲解
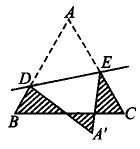
例1、(1)如图所示,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为___________cm.
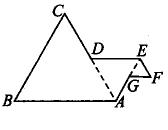
(2)如图,△ABC、△ADE及△EFG都是等边三角形,D和G分别为AC和AE的中点,若AB=4,则图形ABCDEFG外围的周长是( )
A.12 B.15
C.18 D.21
答案:(1)3 (2)B
例2、(1)若一个多边形内角和等于1260°,则该多边形边数是_________.
(2)若一个正多边形的每一个外角都是30°,则这个正多边形的内角和等于_________度.
(3)一个多边形的内角和比它的外角和的3倍少180°.这个多边形的边数是( )
A.5 B.6
C.7 D.8
(4)一个多边形的每个外角都相等,且比它的内角小140°,这个多边形是_________边形.
(5)过多边形的一个顶点可以引9条对角线,那么这个多边形的内角为( )
A.1620° B.1800°
C.1980° D.2160°
答案:
(1)9 (2)1800 (3)C (4)十八 (5)B
例3、(1)如图,分别以四边形ABCD的四个顶点为圆心,半径为R作四个互不相交的圆,则图中阴影部分的面积之和是_________.
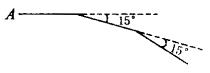
(2)如图,小亮从A点出发前进10m,向右转15°,再前进10m,又向右转15°,……,这样一直走下去,他第一次回到出发点A时,一共走_________m.
答案:
(1)πR2 (2)240
例4、四边形ABCD中,∠A∶∠B∶∠C=3∶2∶1,∠A=∠D.求这个四边形四个内角的度数.
答案:
∠A=120°,∠B=80°,∠C=40°,∠D=120°
例5、已知两个多边形的内角总和为1800°,且两多边形的边长之比为2∶5.求这两个多边形的边数.
答案:
设两个多边形的边数分别为2x和5x,
(2x-2)·180°+(5x-2)·180°=1800°
得x=2.
2x=4,5x=10.
所以这两个多边形的边数分别为4和10.
例6、一个同学在进行多边形内角和计算时,求得内角和为2750°,当发现错了之后,重新检查,发现少加了一个内角.问这个内角是多少度?求这个多边形的边数.
解:
设这个内角是α度,这个多边形的边数为n,则
(n-2)·180°=2750°+α,
∴n-2=15+
.
∵n-2是正整数且0<α<180°,
∴α=130°,n=18.
∴这个内角是130°,这个多边形的边数是18.
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -