| 镶嵌及三角形的有关知识的综合运用 |
主编:黄冈中学数学集体备课组
一、知识归纳
平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做用多边形覆盖平面(或平面镶嵌)的问题.
任意三角形、任意四边形、正六边形可以单独进行平面镶嵌.
二、例题讲解
例1、(1)单独使用正三角形、正方形、正六边形、正八边形四种地砖,不能镶嵌(密铺)地面是__________.
(2)用相同的正多边形拼地板时,只有__________、__________、__________三种正多边形能够单独拼成.
(3)用正三角形和正四边形作平面镶嵌,在一个顶点周围,可以有__________个正三角形和__________个正四边形.
(4)用正三角形和正六边形镶嵌,在每个顶点处有__________个正三角形和__________个正六边形,或在每个顶点处有__________个正三角形和__________个正六边形.
(5)从正三角形、正四边形、正六边形中选一种,再在其他正多边形中选一种,请画出用这两种不同的正多边形镶嵌成一个平面图形(草图);并探究这两种正多边形共能镶嵌成几种不同的平面图形?
答案:
(1)正八边形
(2)正三角形 正方形 正六边形
(3)3 2
(4)2 2,4 1
(5)3个正三角形和2个正四边形;4个正三角形和1个正六边形;2个正三角形和2个正六边形,图略
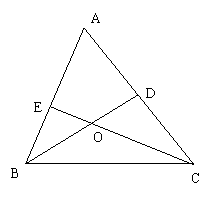
例2、(1)如图,△ABC中,BD、CE分别平分∠ABC、∠ACB,BD、CE相交于点O,则∠BOC与∠A的关系是__________.
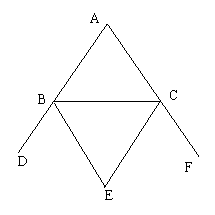
(2)如图,△ABC中,BE平分∠CBD,CE平分∠BCF,则∠E与∠A的关系是__________.
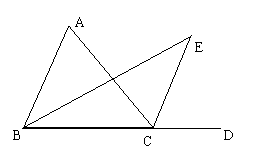
(3)如图,△ABC中,BE平分∠ABC,CE平分∠ACD,则∠E与∠A的关系是__________.
答案:
(1)∠BOC=90°+
∠A
(2)∠E=90°-
∠A
(3)∠E=
∠A
例3、(1)小明有两段篱笆,长分别是3米、5米,如果他要围一个三角形的鸡笼,则还需一段多长的篱笆?
(2)已知△ABC的三边长均为整数,且最长边为5,则这样的三角形共有几个?
(3)小强想把一根木棒截成三段,使其围成一个等腰三角形,若木棒长为1.2米,则腰长的取值范围是__________.
(4)将长为15厘米的木棒截成长为整数的三段,使它们能构成一个三角形,问有几种不同的截法?
答案:
(1)长2米至8米之间(不包括2米和8米)
(2)5,5,5;5,5,4;5,5,3;5,5,2;5,5,1;
5,4,4;5,4,3;5,4,2;
5,3,3.共有9个这样的三角形.
(3)0.3<x<0.6
(4)5,5,5;7,7,1;6,6,3;7,6,2;
6,5,4;7,5,3;7,4,4.
共有七个不同的三角形.
(提示:三角形中最长边的取值范围是
≤最长边≤
,其中c指三角形周长.)
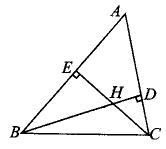
例4、如图,在△ABC中,∠A∶∠ABC∶∠ACB=3∶4∶5,BD、CE分别是AC、AB边上的高,BD、CE相交于点H,求∠BHC的度数.
答案:∠BHC=135°
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -