例、若a、b都是正整数，且143a＋500b＝2001，则a＋b的值是____________．
分析：
首先将143a＋500b＝2001变形得a＝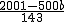
，根据条件a、b都是正整数，即可得b可能为1，2，3，然后分别分析，求得a的值，即可求得a＋b的值．
解：∵a、b都是正整数，且143a＋500b＝2001，
∴a＝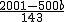
≥1，
∴b≤3.716，
∴若b＝1，则a＝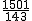
（舍去），
若b＝2，则a＝7，则a＋b＝9，
若b＝3，则a＝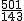
（舍去），
∴a＋b的值是9．
故答案为：9．
点评：
此题考查了二元一次方程的求解方法．解题的关键是由143a＋500b＝2001变形用b表示出a的值，然后分析求得b可能为1，2，3，注意分类讨论思想的应用．
例2、小明给小刚出了一道数学题，题目是：“二元一次方程组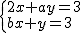
的解是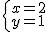
，你能求出我原来的方程组吗？若能，求出原方程组，并求4b2－3a＋2001的值；若不能，说明理由．”请你帮助小刚完成解答．
分析：
把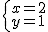
代入方程组即可得到一个关于a，b的方程组，解方程组即可求解得a，b的值，即可得到原方程组，求得代数式的值．
解：能．理由如下：
因为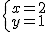
是方程组
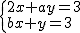的解，
所以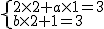
，
解得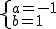
所以原方程组为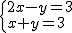
．
∴4b2－3a＋2001＝4×12－3×（－1）＋2001＝2008．
点评：本题主要考查了方程组的解的定义，正确解方程组是关键．
