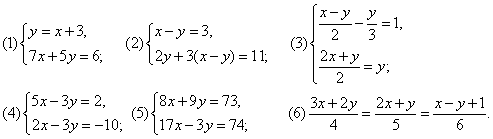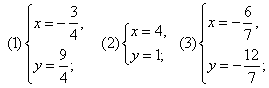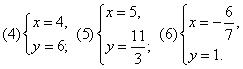| 二元一次方程组的解法 |
主编:黄冈中学数学集体备课组
一、知识归纳
1、代入消元法:把二元一次方程组中一个方程的一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解.这种方法叫做代入消元法,简称代入法.
2、加减消元法:两个二元一次方程中同一未知数的系数互为相反数或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程.这种方法叫做加减消元法,简称加减法.
二、例题讲解
例1、(1)解方程组
的最佳方法是( )
A.由①得
,再代入②
B.由②得
,再代入①
C.由①得3m=7+4n,再代入②
D.由②得9m=10n-25,再代入①
(2)已知二元一次方程
,用含x的代数式表示y为_________.用含y的代数式表示x为_________.
答案:
(1)C
(2)
例2、(1)若
,则x+y=_________;
(2)若
,则x∶y=_________;
(3)已知
,则x与y的关系式为( )
A.3x+2y=1 B.3x-2y=1
C.3x-2y=-1 D.3x-2y=9
答案:
(1)5 (2)2∶1 (3)C
例3、解下列方程组:
答案:
例4、已知
都是方程y=kx+b的解.求当x=5时y的值.
答案:
k=2,b=-3;当x=5时,y=7.
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -