若方程组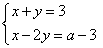
的解x，y都是正数，求a的取值范围．
分析：
先利用加减消元法求出x、y的表达式，再根据x，y都是正数列出不等式组，然后解不等式即可．
解：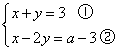
①－②得，3y＝6－a，
解得y＝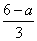
，
把y＝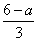
代入②得，x－2×
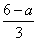＝a－3，
解得x＝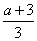
，
∴方程组的解是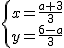
，
∵x，y都是正数，
∴
，
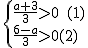由(1)得，a＞－3，
由(2)得，a＜6，
∴a的取值范围－3＜a＜6．
故答案为：－3＜a＜6．
点评：
本题考查了二元一次方程组的解法，以及简单不等式组的解法．关键是要理解二元一次方程组的解的意义．由于两个方程中x的系数相等，所以选择利用加减消元法求出方程组的解较简便．
