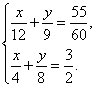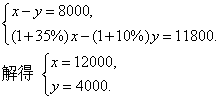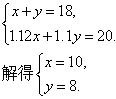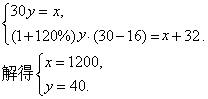| 实际问题与二元一次方程组(二) |
主编:黄冈中学数学集体备课组
一、知识归纳
1、列二元一次方程组解应用题的一般步骤可概括为“审、找、列、解、答”五步,即:
(1)审:通过审题,把实际问题抽象成数学问题,分析已知数和未知数,并用字母表示其中的两个未知数;
(2)找:找出能够表示题意两个相等关系;
(3)列:根据这两个相等关系列出必需的代数式,从而列出方程组;
(4)解:解这个方程组,求出两个未知数的值;
(5)答:在对求出的方程的解做出是否合理判断的基础上,写出答案(包括单位名称).
2、列方程组解应用题的常见题型
(1)和差倍总分问题:较大量=较小量+多余量,总量=倍数×倍量
(2)产品配套问题:加工总量成比例
(3)行程问题:路程=时间×速度
①相遇问题:路程和=相遇时间×速度和
②追及问题:路程差=追及时间×速度差
(4)航速问题:此类问题分为水中航速和风中航速两类
①顺流(风):航速=静水(无风)中的速度+水(风)速
②逆流(风):航速=静水(无风)中的速度-水(风)速
(5)工程问题:工作量=工作效率×工作时间
一般分为两种,一种是一般的工程问题;另一种是工作总量是单位1的工程问题
(6)增长率问题:原量×(1+增长率)=增长后的量,原量×(1+减少率)=减少后的量
(7)浓度问题:溶液×浓度=溶质
(8)银行利率问题:
免税利息=本金×利率×时间
税后利息=本金×利率×时间—本金×利率×时间×税率
(9)利润问题:利润=售价—进价,利润率=(售价—进价)÷进价×100%
(10)盈亏问题:关键从盈(过剩)、亏(不足)两个角度把握事物的总量
(11)数字问题:首先要正确掌握自然数、奇数偶数等有关的概念、特征及其表示
(12)几何问题:必须掌握几何图形的性质、周长、面积等计算公式
(13)年龄问题:抓住人与人的岁数是同时增长的
二、例题讲解
例1、(1)一船顺水航行45千米需要3小时,逆水航行65千米需要5小时,若设船在静水中的速度为x千米/时,水流的速度为y千米/时,则x,y的值为( )
A.x=13,y=2 B.x=14,y=1
C.x=15,y=1 D.x=14,y=2
(2)某学生骑自行车从学校去县城,先以每小时12千米的速度下山,而后以每小时9千米的速度通过平路到达县城,共用去55分钟;返回时,他以每小时8千米的速度通过平路,再以每小时4千米的速度上山回到学校,用去1小时30分钟,学校到县城的距离是__________.
(3)甲、乙两人在200米的环形跑道上练竞走,当他们都从某处同时出发背向行走时每30秒钟相遇一次;同向行走时,每隔4分钟相遇一次,则两人的速度分别为__________.
答案:
(1)B
(2)解:设坡路为x千米,平路为y千米.
依题意有方程组
解得
所以学校到县城的路程为x+y=9千米.
(3)设甲、乙二人的速度分别为x米/分,y米/分.
则
,解之得
所以甲、乙两人的速度分别是225米/分、175米/分.
例2、(1)王阿姨和李奶奶一起去超市买菜,王阿姨买西红柿、茄子、青椒各1kg,共花12.8元,李奶奶买西红柿2kg、茄子1.5kg,共花15元,已知青椒每千克4.2元,请你求出每千克西红柿、茄子各多少元?
(2)在当地农业技术部门指导下,小明家增加种植菠萝的投资,使今年的菠萝喜获丰收,下面是小明爸爸、妈妈的一段对话.

请你用学过的知识帮助小明算出他们家今年菠萝的收入.(收入-投资=净赚)
答案:
(1)4.2 4.4
(2)解:设去年收入为x元,投资为y元,则
所以今年的收入为(1+35%)x=12000×1.35=16200(元).
例3、(1)“种粮补贴”惠农政策的出台,大大激发了农民的种粮积极性,某粮食生产专业户去年计划生产小麦和玉米共18吨,实际生产了20吨,其中小麦超产12%,玉米超产10%,该专业户去年实际生产小麦、玉米各多少吨?
(2)某公司接受一批产品定货,按定额预计划30天可以完成,经管理改革和技术革新后,劳动生产效率提高了120%,结果提前16天完成任务,并超产32件,求该公司接受的加工任务是多少件?原来每天的定额是多少件?
答案:
(1)解:设去年实际生产小麦x吨,玉米y吨,则
1.12x=11.2,1.1y=8.8.
所以该专业户去年实际生产小麦11.2吨,生产玉米8.8吨.
(2)解:设该公司接受的加工任务为x件,原来每天的定额是y件,则
所以该公司接受的加工任务为1200件,原来每天的定额是40件.
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -