例1、参加世界杯决赛的32支球队在第一轮比赛中，平均分成8个小组分别进行单循环赛（每两个队之间打一场比赛）每小组前两名进入16强，已知各小组的得分情况如下表：（胜一场得3分，平一场得1分，输一场得0分）
 |
A组 |
B组 |
C组 |
D组 |
E组 |
F组 |
G组 |
H组 |
第一名 |
7 |
9 |
9 |
7 |
7 |
5 |
7 |
7 |
第二名 |
5 |
4 |
4 |
4 |
5 |
5 |
4 |
6 |
第三名 |
4 |
4 |
4 |
3 |
4 |
4 |
3 |
3 |
第四名 |
0 |
0 |
0 |
3 |
0 |
1 |
3 |
1 |
试求在第一轮比赛中打出胜负和打平的场次各是多少？
分析：
由题目提供数据信息已知：
（1）32支球队，分成8个小组，每组4个队，比赛场次有3＋2＋1=6场次，8个小组共比赛6×8=48场次；
（2）比赛打出的胜负场次相等，因此两队打成胜负的每一场共得分3＋0=3分，打平的共得分为1＋1=2分；
（3）由表格中提供的各小组得分情况可知，8个小组比赛48场次总分为：
16＋17＋17＋17＋16＋15＋17＋17=132（分）
掌握以上信息后，很容易列出方程组解此应用题.
解：
设在第一轮比赛中打出胜负的场次为x，打平的场次为y.
根据题意，得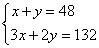
解此方程组，得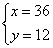 
答：在第一轮的比赛中打出胜负的是36场次，打平的是12场次.
例2、有三块牧场，草长得一样密一样快，面积分别为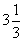
公顷，10公顷和24公顷，第一块12头牛可吃4星期，第二块21头牛可吃9星期，第三块可供多少头牛吃18个星期？
分析：
问题中涉及的草量问题有两种，一是原有草量，二是每公顷每周的新生草量.但每头牛每星期吃掉的草量应为一个定值.据此可找出相等关系.
解：
设牧场每公顷原有草xt，每星期新生草yt，每头牛每周吃草at，根据题意得
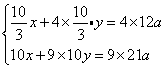
原方程组化简得：
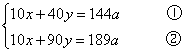
②－①得，50y=45a
∴ y=0.9a
将y=0.9a代入①得
10x＋40×0.9a=144a
∴ x=10.8a
∴ 
∴ 
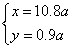
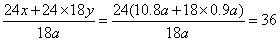
∴第三块牧场可供36头牛吃18个星期.
