| 不等式 |
主编:黄冈中学数学集体备课组
一、知识归纳
1、不等式:用“<”或“>”或“≥”或“≤”或“≠”号表示大小关系的式子,叫做不等式.
2、不等式的解:把使不等式成立的未知数的值叫做不等式的解.
3、不等式的解集:使不等式成立的未知数的取值范围叫做不等式的解的集合,简称解集.
4、一元一次不等式:含有一个未知数,未知数的次数是1的不等式,叫做一元一次不等式.
5、不等式的性质:
性质(1):不等式两边加(或减)同一个数(或式子),不等号的方向不变;
性质(2):不等式两边乘(或除以)同一个正数,不等号的方向不变;
性质(3):不等式两边乘(或除以)同一个负数,不等号的方向改变.
二、例题讲解
例1、(1)在数学表达式中:①-1<0,②3m-2n>0,③x=4,④x≠7,⑤m+n,不等式是__________ (填序号) .
(2)下列各式中,是一元一次不等式的是( )
A.x+y-2=0 B.3x+1≤2+x
C.x2-x>0 D.4x-5=x+4
(3)下列按要求列出的不等式,不正确的是( )
A.x的3倍与1的差不小于2 3x-1≥2
B.x与4的和至少是x的3倍 x+4>3x
C.x的
不大于x的
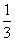
D.a的
倍与4的和最多是3
+4≤3
(4)下列说法中,正确的是( )
A.x=2是不等式3x>5的一个解
B.x=2是不等式3x>5的解集
C.x=2是不等式3x>5的唯一解
D.x=2是不等式2x>5的解
(5)2a-3x2+2a>1是关于x的一元一次不等式,则a=___________,不等式的解集为_________.
(6)如果a<b<0,下列不等式中错误的是( )
A.ab>0 B.a+b<0
C.
D.a-b<0
答案:
(1)①②④ (2)B (3)B (4)A (5)
(6)C
例2、(1)若
,则a_____b;若5x-5y<0,则x_____y.
(2)已知m>n,a为任意有理数,则-(3a-5m) __________-(3a-5n).
(3)若-x<-y,则x_____y;若(m2+1)x>(m2+1)y,则x____y.
(4)由ax>b,得
,则a__________0;由ac2>bc2,可得a______b.
答案:
(1)> <
(2)>
(3)> >
(4)< >
例3、利用不等式的基本性质求下列不等式的解集,并在数轴上表示出来:
(1)x+
<3;(2)3x+2≤8;(3)
.
例4、(1)若三角形的三边长为3,4,x-1,则x的取值范围是( )
A.0<x<8 B.2<x<8
C.0<x<6 D.2<x<6
(2)已知一个等腰三角形的底边长为5,这个等腰三角形的腰长为x,则x的取值范围是( )
A.0<x<
B.x≥
C.x>
D.0<x<10
答案:(1)B (2)C
例5、根据等式和不等式的基本性质,我们可以得到比较两数大小的方法:
(1)若A-B>0,则A__________B;
(2)若A-B=0,则A__________B;
(3)若A-B<0,则A__________B.
这种比较大小的方法称为“求差法比较大小”,请运用这种方法尝试解决下面问题:
(4)若A=4+3a2-2b+b2,B=3a2-2b+1,试比较A与B的大小.
答案:
(1)> (2)= (3)<
(4)A-B=4+3a2-2b+b2-(3a2-2b+1)=3+b2>0,
∴A>B.
高一全科点睛班课程 高一全科强化班课程 高二全科全年强化班 高三全科强化班课程 初一全科强化班课程 初一全科点睛班课程 初二全科强化班视频 初二全科点睛班课程 初三全科强化班 全科巨无霸同步提高课程 小学全年全科强化班
- 返回 -