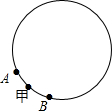
例、如图，A和B两个小机器人，自甲处同时出发相背而行，绕直径为整数米的圆周上运动，15分钟内相遇7次，如果A的速度每分钟增加6米，则A和B在15分钟内相遇9次，问圆周直径至多是多少米？至少是多少米？（取π＝3.14）
分析：
行程中的相遇问题，从小学开始就是重要的应用题型，属基本题型.其中路程、时间与速度的关系是基本知识．
解：
由于圆的直径为D，则圆周长为πD．设A和B的速度和是每分钟V米，一次相遇所用的时间为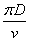
分；他们15分钟内相遇7次，用数学语言可以描述为
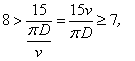①
如果A的速度每分钟增加6米，A加速后的两个机器人的速度和是每分钟
米，则A和B在15分钟内相遇9次，用数学语言可以描述为
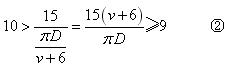
由①，得
由②，得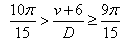
，
上面两式相加，则有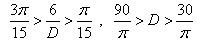
，
所以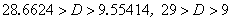
.
已知“圆的直径为整数米”，所以，圆周直径至多是28米，至少是10米.
点评：
将行程问题与不等式的整数解联系起来，使行程问题的老题型有了新意，运算与表达难度对初一学生适中，可以综合考查学生的数学素养与数学能力．解决本题的关键在于基本技能的综合运用．
