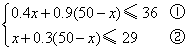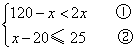| 不等式(组)的应用 |
主编:黄冈中学数学集体备课组
例题讲解
例1、(1)某次数学测验中共有16道题目,评分办法:答对一道得6分,答错一道扣2分,不答得0分.某学生有一道题未答,那么这个同学至少要答对__________道题,成绩才能在60分以上.
(2)有含盐5%的盐水10千克,要用15千克的盐水和它混合,使混合后的盐水浓度不低于8%,且不高于14%,则所选15千克的盐水的浓度P的范围是( )
A.10%≤P≤14% B.10%≤P≤20%
C.5%≤P≤8% D.8%≤P≤14%
答案:(1)12 (2)B
例2、某班有住宿生若干人,分住若干间宿舍,若每间住4人,则还余20人无宿舍住;若每间住8人,则有一间宿舍不空也不满,求该班住宿生人数和宿舍间数.
解:设有x间宿舍,则
0<4x+20-8(x-1)<8,
0<-4x++28<8,
-28<-4x<-20,
5<x<7.
∵x为整数,
∴x=6.
∴4x+20=24+20=44.
∴该班住宿生人数为44人,有6间宿舍.
例3、某城市平均每天生产垃圾700t,由甲、乙两个垃圾处理厂处理,已知甲处理厂每小时可处理垃圾55t,需费用550元;乙处理厂每小时可处理垃圾45t,需费用495元.
(1)甲、乙两厂同时处理该城市的垃圾,每天多少个小时才能完成?
(2)若该城市每天处理垃圾的费用不得超过7370元,那么甲厂每天至少处理垃圾多少小时?
解:
(1)
.
(2)设甲厂每天处理垃圾x小时,则
550x+
×495≤7370
55x≥330
x≥6
∴甲厂每天至少处理垃圾6小时.
例4、七(2)班共有50名学生,老师安排每人制作一件A型或B型的陶艺品,学校现有甲种制作材料36kg,乙种制作材料29kg,制作A、B两种型号的陶艺品用料情况如下表:
需甲种材料
需乙种材料
1件A型陶艺品
0.9kg
0.3kg
1件B型陶艺品
0.4kg
1kg
(1)设制作B型陶艺品x件,求x的取值范围;
(2)请你根据学校现有的材料分别写出七(2)班制作A型和B型陶艺品的件数.
解:
(1)
由①得:x≥18
由②得:x≤20
∴18≤x≤20
(2)∵18≤x≤20且x为整数
∴x=18,19,20
∴50-x=32,31,30
∴制作B型陶艺品18件,A型陶艺品32件,
或B型陶艺品19件,A型陶艺品31件,
或B型陶艺品20件,A型陶艺品30件.
例5、为支持四川抗震救灾,重庆市A、B、C三地现在分别有赈灾物资100吨、100吨、80吨,需要全部运往四川重灾地区的D、E两县,根据灾区的情况,这批赈灾物资运往D县的数量比运往E县的数量的2倍少20吨.
(1)求这批赈灾物资运往D、E两县的数量各是多少?
(2)若要求C地运往D县的赈灾物资为60吨,A地运往D县的赈灾物资为x吨(x为整数),B地运往D县的赈灾物资数量小于A地运往D县的赈灾物资数量的2倍,其余的赈灾物资全部运往E县,且B地运往E县的赈灾物资数量不超过25吨,则A、B两地的赈灾物资运往D、E两县的方案有几种?
(3)已知A、B、C三地的赈灾物资运往D、E两县的费用如下表:
A地
B地
C地
运往D县的费用(元/吨)
220
200
200
运往E县的费用(元/吨)
250
220
210
为及时将这批赈灾物资运往D、E两县,某公司主动承担运送这批赈灾物资的总费用,在(2)问的要求下,该公司承担运送这批赈灾物资的总费用最多是多少?
解:
(1)设运往E县的数量为a吨,则
a+2a-20=100+100+80
3a=300
a=100
∴2a-20=180
∴运往D、E两县的数量分别为180吨、100吨.
(2)列不等式组
由①得:x>40
由②得:x≤45
∴40<x≤45
又x为整数
∴x=41,42,43,44,45
∴有5种方案.
(3)设总费用为W元,则
W=220x+200(120-x)+200×60+250(100-x)+220(x-20)+210×20
=-10x+60800
当x=41时,Wmax=-410+60800=60390元.
高一全科点睛班课程 高一全科强化班课程 高二全科全年强化班 高三全科强化班课程 初一全科强化班课程 初一全科点睛班课程 初二全科强化班视频 初二全科点睛班课程 初三全科强化班 全科巨无霸同步提高课程 小学全年全科强化班
- 返回 -