例1、某钱币收藏爱好者想把3.50元纸币兑换成1分、2分、5分的硬币，他要求硬币总数为150枚，且每种硬币不少于20枚，5分的硬币要多于2分的硬币，请你据此设计兑换方案.
解：
设兑换成的1分，2分，5分硬币分别为x枚、y枚、z枚，
则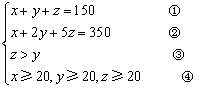
由①、②得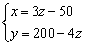
将x、y代入③、④得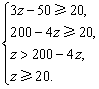
解得40<z≤45
故整数z=41，42，43，44，45.
由此列出x，y的对应值，于是得到5种方案：
（x，y，z）为（73，36，41）或（76，32，42）或（79，28，43）或（82，24，44）或（85，20，45）.
例2、某工厂有一批产品可用大小两种包装箱包装，表中表示三种不同的装箱方案：
| |
用大箱装 |
用小箱装 |
用箱总数 |
方案一 |
360件 |
360件 |
75个 |
方案二 |
600年 |
120件 |
|
方案三 |
480件 |
240件 |
70个 |
（1）将上表补充完整；
（2）如果每只大箱的包装费比每只小箱的包装费高k%（25≤k≤55），试确定哪种包装方案能使这批产品的包装费最低？
解：
设大箱每只装x件，小箱每只装y件，则
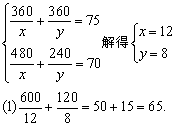
故填65.
（2）设每只小箱的包装费为a元，则
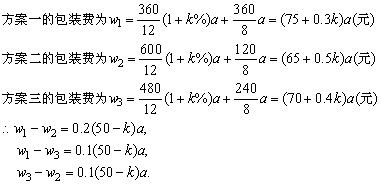
而25≤k≤55.
故①当25≤k<50时，w1－w2>0,w3－w2>0,∴w2<w1,w2<w3，此时方案二费用最低.
②当k=50时，w1=w2=w3，此时，三种方案费用一样.
③当50<k≤55时，w1－w2<0,w1－w3<0,即w1<w2,w1<w3，此时方案一费用最低.
