| 平行线及平行线的判定方法(1) |
主编:黄冈中学数学集体备课组
一、知识归纳
1、平行:如果两条直线a与b不相交,那么这两条直线a与b互相平行,记作a//b.
2、平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
3、平行公理推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
即如果a//b,b//c,那么a//c.
4、判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线互相平行.
简单说成:同位角相等,两直线平行.
5、在同一平面内,两条不同的直线的位置关系只有2种,就是相交和平行.
二、例题讲解
例1、(1)在同一平面内,下列说法正确的有( )
①过两点有且只有一条直线;
②两条不同的直线有且只有一个交点;
③过一点有且只有一条直线与已知直线垂直;
④过一点有且只有一条直线与已知直线平行.
A.1个 B.2个 C.3个 D.4个
(2)下列各种说法,正确的是( )
①在平面内的两条线段,如果没有公共点,那么这两条线段平行;
②如果两条射线平行,那么这两条射线没有公共点;
③如果两条直线没有公共点,那么这两条直线平行;
④在平面内的两条直线,不相交则一定平行
A.②③④ B.②③ C.①② D.②④
答案:(1)B (2)D
例2、(1)如图,若∠1=∠2,则_________//_________;
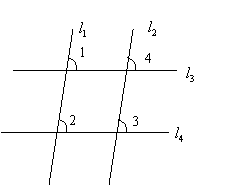
若∠2=∠3,则____∥_____;
若∠3=_________,则l3//l4;
若∠4=_________,则l1//l2.
(2)已知l1、l2、l3被l4所截,若要使l1//l3,则添加的一个条件是( )
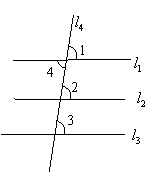
A.∠1=∠2 B.∠2=∠3
C.∠1=∠3 D.∠1=∠4
(3)如图,直线MN分别交AB、CD于E、F,∠MFD=50°,EG平分∠MEB,则当∠MEG=_________时,AB//CD.
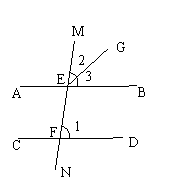
答案:
(1)l3 l4;l1 l2;∠4;∠1
(2)C
(3)25°
提示:当∠MEB=∠MFD时,AB∥CD
即∠1=∠2+∠3
又EG平分∠MEB, ∴∠2=∠3
∴2∠2=∠1=50°,∴∠2=25°
例3、(1)如图,∠2=3∠1,且∠1+∠3=90°,试说明AB//CD.
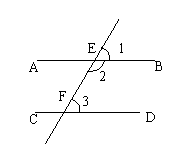
∵∠1+∠2=180°,且∠2=3∠1,
∴∠1+3∠1=180°,∴∠1=45°
又∠1+∠3=90°,∴∠3=45°
∴∠1=∠3,∴AB//CD.
(2)如图,已知∠1=∠2,AF平分∠EAQ,BC平分∠ABN,怎样说明PQ//MN.
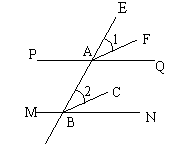
解:
∵AF平分∠EAQ,BC平分∠ABN,
∴∠EAQ=2∠1,∠EBN=2∠2,
又 ∠1=∠2,∴∠EAQ=∠EBN
∴PQ∥MN
(3)如图,已知直线a、b、c被直线d、e所截,∠1=∠2,∠3=∠4,那么直线a与直线c平行吗?为什么?
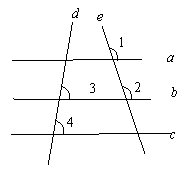
解:
直线a与直线c平行.理由如下:
∵∠1=∠2,∴a∥b
又∠3=∠4,∴b∥c
∴a∥c(平行公理推论)
高一全科点睛班课程 高一全科强化班课程 高二全科全年强化班 高三全科强化班课程 初一全科强化班课程 初一全科点睛班课程 初二全科强化班视频 初二全科点睛班课程 初三全科强化班 全科巨无霸同步提高课程 小学全年全科强化班
- 返回 -