探索与发现:
(1)若直线a1⊥a2,a2∥a3,则直线a1与a3的位置关系是____________,请说明理由.
(2)若直线a1⊥a2,a2∥a3,a3⊥a4,则直线a1与a4的位置关系是_____________(直接填结论,不需要证明)
(3)现在有2011条直线a1,a2,a3,…,a2011,且有a1⊥a2,a2∥a3,a3⊥a4,a4∥a5…,请你探索直线a1与a2011的位置关系.
分析:
(1)根据两直线平行,同位角相等得出相等的角,再根据垂直的定义解答;
(2)根据(1)中结论即可判定垂直;
(3)根据规律发现,直线a1与脚码是偶数的直线互相平行,与脚码是奇数的直线互相垂直,根据此规律即可判断.
解:(1)a1⊥a3.
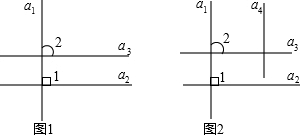
理由如下:如图1,∵a1⊥a2,
∴∠1=90°,
∵a2∥a3,
∴∠2=∠1=90°,
∴a1⊥a3;
(2)同(1)的解法,如图2,直线a1与a4的位置关系是:a1∥a4;
(3)直线a1与a3的位置关系是:a1⊥a3,
直线a1与a4的位置关系是:a1∥a4,
以此类推,直线a1与a2011的位置关系是:a1⊥a2011.
点评:
本题考查了平行公理的应用,作出图形更有利于规律的发现以及规律的推导.