例1、我们知道,光线从空气射入水中会发生折射现象,光线从水中射入空气中,同样会发生折射现象.如图,是光线从空气中射入水中,再从水中射入空气中的示意图.由于折射率相同,因此已知∠1=∠4,∠2=∠3.请你用所学知识来判断c与d是否平行?并说明理由.
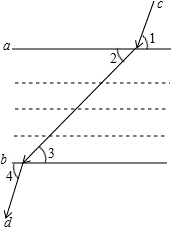
分析:
欲证明c∥d,结合图形只要先证明∠2+∠5=∠3+∠6,再利用内错角相等,两直线平行判定c∥d.
解:c∥d;
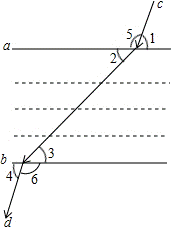
如图,∵∠1+∠5=∠4+∠6,∠1=∠4,
∴∠5=∠6,
∵∠2=∠3,
∴∠2+∠5=∠3+∠6,
∴c∥d(内错角相等,两直线平行).
点评:
正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
例2、已知:如图,六边形ABCDEF中,∠A+∠B+∠C=∠D+∠E+∠F,猜想六边形ABCDEF中必有两条边是平行的.
(1)根据图形写出你的猜想:___________∥___________;
(2)请证明你在(1)中写出的猜想.
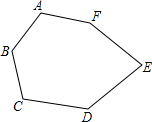
分析:
(1)根据多边形的内角和以及已知条件求出∠A+∠B+∠C=360°,连接AC,根据三角形的内角和等于180°,可以求出∠FAC+∠ACD=180°,然后根据同旁内角互补,两直线平行即可证明AF∥CD;
(2)根据(1)中的分析思路写出证明过程即可.
(1)解:猜想:AF∥CD;
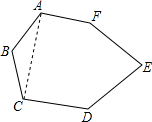
(2)证明:如图,连接AC,
∵∠A+∠B+∠C=∠D+∠E+∠F,
∴∠A+∠B+∠C=(6-2)·180°÷2=360°,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠FAC+∠ACD=360°-180°=180°,
∴AF∥CD(同旁内角互补两直线平行).
点评:
本题考查了多边形的内角和公式,三角形的内角和等于180°,以及同旁内角互补,两直线平行的判定,作辅助线求出∠FAC+∠CAF=180°是解题的关键.