| 平行线的性质 |
主编:黄冈中学数学集体备课组
一、知识归纳
性质1 两条平行线被第三条直线所截,同位角相等;
性质2 两条平行线被第三条直线所截,内错角相等;
性质3 两条平行线被第三条直线所截,同旁内角互补.
简单说成:
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补.
二、例题讲解
例1、(1)如图,AB//CD,直线EF与AB、CD分别相交于G、H,∠AGE=60°,则∠EHD的度数是( )
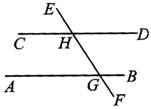
A.30° B.60° C.120° D.150°
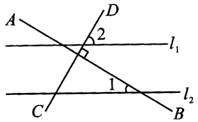
(2)如图,直线l1//l2,AB⊥CD,∠1=34°,那么∠2的度数是________.
(3)如图,已知∠1=∠2,∠3=80°,则∠4等于( )
A.80° B.70° C.60° D.50°
(4)如图,是明明养的小乌龟上的一块花纹,DE//FG,BC//DE,EF//DC,DC//AB,则∠B与∠F的关系是_____________.
答案:(1)C (2)56° (3)A (4)∠B=∠F
例2、(1)如图,已知AB//EF//CD,EG//DB,图中与∠1相等的角(∠1除外)共有( )
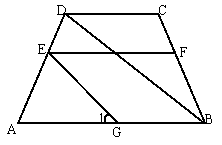
A.6个 B.5个 C.4个 D.3个
(2)如图,是赛车跑道的一段示意图,其中AB//DE,测得∠B=140°,∠D=120°,则∠C的度数为( )
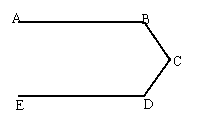
A.120° B.100° C.140° D.90°
(3)在同一平面内有两个角,它们有一条边在同一直线上,另一边互相平行,那么这两个角的关系是( )
A.相等 B.互补 C.相等且互补 D.相等或互补
答案:(1)B (2)B (3)D
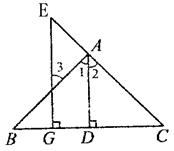
例3、如图,已知AD⊥BC于D,EG⊥BC于G,且∠E=∠3,试说明AD平分∠BAC的理由.
解:
∵AD⊥BC,EG⊥BC,
∴AD∥EG,
∴∠E=∠2,∠3=∠1
又∠E=∠3,∴∠1=∠2
∴AD平分∠BAC
例4、已知,如图,∠1=∠2,∠A=∠F,试说明为什么∠C=∠D?
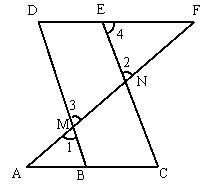
解:
∵∠A=∠F,
∴DF∥AC,∴∠C=∠4
∵∠1=∠2,∠1=∠3,
∴∠2=∠3,
∴DB∥EC,
∴∠D=∠4
又 ∠C=∠4
∴∠C=∠D
例5、如图,已知∠1+∠2=180°,∠B=∠3,试判断∠AED与∠C的大小关系,并说明理由.
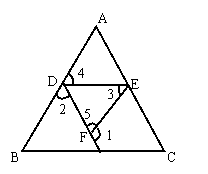
解:
∠AED=∠C.理由如下:
∵∠1+∠2=180°,∠1+∠5=180°
∴ ∠2=∠5,∴AB∥EF
∴∠4=∠3
又 ∠B=∠3,∴∠4=∠B
∴DE∥BC,∴∠AED=∠C
例6、如图,已知AD⊥AB,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°,那么BC⊥AB,说明理由.

解:
∵DE平分∠ADC,CE平分∠BCD
∴∠1=∠3,∠2=∠4
又 ∠1+∠2=90°
∴∠1+∠2+∠3+∠4=180°
即 ∠ADC+∠BCD=180°
∴ AD∥BC
又 AD⊥AB
∴ BC⊥AB
高一全科点睛班课程 高一全科强化班课程 高二全科全年强化班 高三全科强化班课程 初一全科强化班课程 初一全科点睛班课程 初二全科强化班视频 初二全科点睛班课程 初三全科强化班 全科巨无霸同步提高课程 小学全年全科强化班
- 返回 -