例、如图，在平面直角坐标系中，已知三点A（0，a），B（b，0），C（b，c），其中a，b，c满足关系式|a－2|＋（b－3）2＝0，c＝2b－a；
（1）求a，b，c的值；
（2）如果再第二象限内有一点P（m，1），请用含m的式子表示四边形ABOP的面积，若四边形ABOP的面积与△ABC的面积相等，请求出点P的坐标；
（3）若B，A两点分别在x轴，y轴的正半轴上运动，设∠BAO的邻补角的平分线和∠ABO的邻补角的平分线相交于第一象限内一点Q，那么，点A，B在运动的过程中，∠Q的大小是否会发生变化？若不发生变化，请求出其值，若发生变化，请说明理由．
分析：
（1）由绝对值、完全平方均≥0而求得．（2）由三角形ABC和四边形ABOP面积相等，从而代入m值来求得．（3）因为∠AOB为定值，把所求角度转化成角AOB，所以证明所求角度为定值．
解：（1）∵|a－2|＋（b－3）2＝0，
∴a－2＝0，b－3＝0，
即a＝2，b＝3，
又∵c＝2b－a，
∴c＝2×3－2＝4；
（2）由题意：S△ABC＝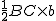
＝
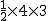＝6，
S四边形ABOP＝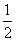
×AO×|m|+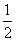×AO×|b|＝
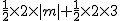＝|m|＋3，
由题意S四边形ABOP＝S△ABC，
∴|m|＋3＝6，
即m＝±3，
∵点P在第二象限，
∴点P（－3，1）；
（3）∠AQB为定值．
证明：∵2∠BAQ＝∠AOB＋∠ABO，2∠ABQ＝∠AOB＋∠OAB，
∴2（∠BAQ＋∠ABQ）＝2∠AOB＋∠ABO＋∠OAB，
∠BAQ＋∠ABQ＝∠AOB＋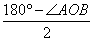
＝135°，
∴∠BAQ＋∠ABQ的大小为定值，
∴∠AQB＝180°－（∠BAQ＋∠ABQ）=45°，故∠AQB为定值．
