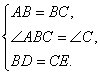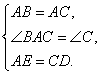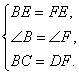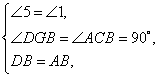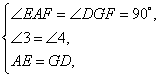| 等边三角形 |
主编:黄冈中学数学集体备课组
一、定义:三条边都相等的三角形叫做等边三角形.
二、性质:
1、具有等腰三角形所有性质.
2、等边三角形三边、三内角分别相等,且每一个内角都等于60°.
三、判定:
1、利用定义.
2、证三个角都相等.
3、有一个角是60°的等腰三角形是等边三角形.
四、直角三角形性质
在直角三角形中,30°角所对的直角边等于斜边的一半.
例1、如图,等边△ABC中,BD=CE,AD与BE交于点P.求∠APE的度数.
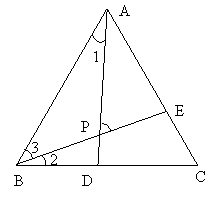
解:
∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠C=60°.
在△ABD和△BCE中,
∴△ABD≌△BCE(SAS),
∴∠1=∠2,
∴∠APE=∠3+∠1=∠3+∠2=60°.
总结:若在等边三角形两边上截取相等的线段,则构造的三角形全等.
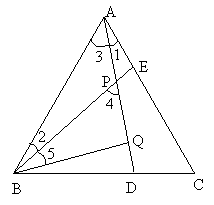
变式:如图,在等边△ABC中,AE=CD,AD、BE交于点P,BQ⊥AD于Q,PQ=3,PE=1.求AD的长.
解:∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠C=60°,
在△ABE和△CAD中,
∴△ABE≌△CAD(SAS),
∴BE=AD,∠1=∠2,
∴∠4=∠2+∠3=∠1+∠3=60°.
又BQ⊥AD,∴∠5=30°,
∴BP=2PQ=6,
∴AD=BE=BP+PE=7.
例2、如图,△ABC为等边三角形,延长BA到E,使AE=BD.求证:CE=DE.
证明:延长BD至F,使DF=BC,连EF,
∵△ABC是等边三角形,
∴AB=BC,∠B=60°,
∴DF=AB,
∵AE=BD,
∴AB+AE=BD+DF,
∴BE=BF.
∴△BEF是等边三角形,
∴BE=FE,∠B=∠F=60°.
在△EBC和△EFD中,
∴△EBC≌△EFD(SAS),(视频中△EDF应写成△EFD)
∴CE=DE.
例3、如图,Rt△ABC中,∠ACB=90°,∠1=30°,分别以AB、AC为边向形外作等边△ABD和等边△ACE,连DE交AB于F.求证:DF=FE.
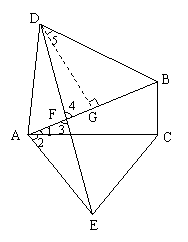
证明:
过D作DG⊥AB于G.
∵△ABD和△ACE是等边三角形,
∴AD=AB,AC=AE,∠2=60°,
而DG⊥AB,∴∠5=30°.
在△DGB和△ACB中,
∴△DGB≌△ACB(AAS),
∴DG=AC,
∴DG=AE.
∵∠1=30°,∠2=60°,
∴∠EAF=90°.
在△AEF和△GDF中,
∴△AEF≌△GDF(AAS),
∴DF=FE.
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -