| 一次函数(二) |
主编:黄冈中学数学集体备课组
例1、某液化气站有一储存量为40吨的液化气储存罐,开始一段时间内打开进气管,不开出气管,在随后一段时间内既开进气管又开出气管,直到装满储存罐时关闭进气管,储存罐中液化气储存量y(吨)关于时间x(分)的函数关系如图所示,则y与x之间的函数关系式是___________.

答案:
例2、某电信公司提供了A、B两种方案的移动通讯费用y(元)与通话时间x(分)之间的关系,则以下说法错误的是( )
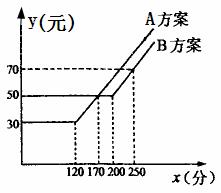
A.若通话时间少于120分,则A方案比B方案便宜20元
B.若通话时间超过200分,则B方案比A方案便宜12元
C.若通讯费用为60元,则B方案比A方案的通话时间多
D.若两种方案通讯费用相差10元,则通话时间是145分或185分
答案:D
例3、某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时内血液中含药量最高,达每毫升6微克(1微克等于10-3毫克),接着逐渐衰减,服药后10小时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随时间x(小时)的变化如图,当成人按规定剂量服药后:

(1)分别求出x≤2和x>2时,y与x之间的函数关系式;
(2)如果每毫升血液中含药量为4微克或4微克以上时在治疗疾病时是有效的,那么这个有效时间是多长?
解:
(1)当x≤2时,设y=k1x,
将(2,6)代入得:6=2k1,∴k1=3,
∴y=3x.
当x>2时,设y=k2x+b,
将(2,6),(10,3)代入得:
(2)令y=3x中y=4,得
;
令
中y=4,得
,
∴有效时间:
.
例4、某空军加油飞机接到命令,立即给另一架正在飞行的运输飞机进行空中加油.在加油过程中,设运输飞机的油箱余油量为Q1吨,加油飞机的加油油箱余油量为Q2吨.加油时间为t分钟,Q1,Q2与t之间的函数图象如图所示,结合图象回答下列问题:

(1)加油飞机的加油油箱中装载了多少吨油?将这些油全部加给运输飞机需多少分钟?
(2)求加油过程中,运输飞机的余油量Q1与时间t的函数关系式;
(3)运输飞机加完油后,以原速继续飞行,需10h到达目的地,油料是否够用?说明理由.
解:
(1)由图象知,加油飞机的加油箱中装载了30吨油,全部加给运输飞机需10分钟.
(2)设Q1=kt+b,把(0,40)和(10,69)代入得:
![]()
∴Q1=2.9t+40(0≤t≤10).
(3)油料够用,理由如下:
运输飞机每小时耗油量![]() 吨.
吨.
∴10h耗油量6×10=60吨<69吨,
∴油料够用.
例5、课间休息时,同学们依次到一个容量为10升的饮水机旁接水0.25升,他们先打开一个饮水管,后来又打开了第二个饮水管.假设接水的过程中每只饮水管出水的速度是匀速的,在不关闭饮水管的情况下,饮水机水桶内的存水量y(升)与接水时间x(分)的函数图象如图所示.

请结合图象回答下列问题:
(1)求存水量y(升)与接水时间x(分)的函数关系式;
(2)如果接水的同学有28名,那么他们都接完水需要几分钟?
解:
(1)当0≤x≤2时,设y=k1x+b1,
将(0,10),(2,9)代入得:
∴y=-0.5x+10(0≤x≤2).
当2<x≤8时,设y= k2x+b2,
将(2,9),(5,4.5)代入得:
∴y=-1.5x+12(2<x≤8),
(2)28名同学需水28×0.25=7(升),
此时水桶存水量10-7=3(升).
令y=-1.5x+12中y=3,
得x=6,
即28名同学接完水需6分钟.
高一全科点睛班课程 高一全科强化班课程 高二全科全年强化班 高三全科强化班课程 初一全科强化班课程 初一全科点睛班课程 初二全科强化班视频 初二全科点睛班课程 初三全科强化班 全科巨无霸同步提高课程 小学全年全科强化班
- 返回 -


