| 图形的旋转 |
主编:黄冈中学数学集体备课组
知识点归纳
1、旋转的概念:
①旋转的定义:在平面内,把一个图形绕着某点转动一个角度的图形变换叫做旋转,这一点叫做旋转中心,转动的角叫做旋转角.
②旋转变换和平移变换一样,只改变图形的位置,不改变图形的形状大小,这两种变换我们都称为全等变换.
③下列生活现象:(1)公园里荡秋千,(2)用扳手钮螺母,(3)两个儿童玩跷跷板等都属于图形旋转.
2、旋转中心和旋转角:如果图形上任意一点P,经过旋转变换对应点为P′,旋转中心为O,那么旋转角为
.
3、旋转的性质
图形的旋转特征是:图形中每一个点都绕着旋转中心旋转了相同的角度;即对应点与旋转中心的连线所成的角等于旋转角;对应点到旋转中心的距离相等;对应线段相等,对应角相等,图形的形状大小都没有发生变化.
4、旋转图形的作图与设计:
旋转作图有三要素:一是旋转中心,二是旋转方向,三是旋转角.
典例讲解
例1、填空题
1、如图,把Rt△ABC斜边AB放在定直线l上,∠CAB=30°,将△ABC按如图方式旋转.
(1)第一次旋转中心是__________,旋转角度为__________.
(2)第二次旋转中心是__________,旋转角度为__________.
答案:(1)点B;120°(2)点C;90°
2、如图,在△ABC中,
,将其绕点B顺时针旋转60°,得到△A1BC1,连接AA1、CC1,则∠A1BC1=__________度,∠ABA1=__________度,∠C1BC=__________度,AC=__________,图中有__________个等边三角形,它们分别是__________.
答案:120,60,60,A1C1,两,△A1AB和△BCC1
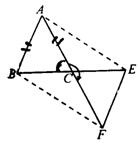
例2、已知:如图在
中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.
(1)试猜想AE与BF有何关系?说明理由.
解:
BF.
理由:∵△ABC绕点O顺时针旋转180°得到△FEC,则△ABC≌△FEC,
且点A、C、F三点共线,点B、C、E三点共线,即AF、BE互相平分,
∴四边形ABFE是平行四边形.
∴AE
BF.
(2)若△ABC的面积为3cm2,求四边形ABFE的面积.
解:
由(1)得四边形ABFE是平行四边形,
∴
.
∵S△ABC=3cm2,∴
=12cm2.
(3)当∠ACB为多少度时,四边形ABFE为矩形?说明理由.
解:
当∠ACB=60°时,四边形ABFE为矩形.理由:
∵AB=AC,∠ACB=60°
∴△ABC是等边三角形,∴AC=BC.
由(1)得AC=CF,BC=CE.
∴AF=BE,由(1)知四边形ABFE是平行四边形,
∴四边形ABFE是矩形.
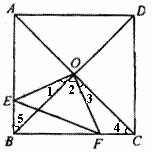
例3、如图,正方形ABCD的对角线相交于点O,OE⊥OF,若AE=8、CF=6,求EF的长.
解:
正方形ABCD,∠BCD=90°
∠4=
,∴∠4=45°,
同理可得:∠5=45°,∴∠4=∠5.
∵∠2+∠3=∠1+∠2=90°,
∴∠3=∠1.
∵OB=OC,∴△OBE≌△OCF(ASA),
∴BE=CF=6,BC=AB=14,
∴BF=8,∵∠EBF=90°,∴EF=
.
例4、已知P为等边△ABC内一点,PA=2,PB=
,PC=4.求△ABC中∠APB的度数.

解:
将△PBC绕点B顺时针旋转60°得到△P′BA,连接PP′.
则△PBC≌△P′BA.
∴BP=BP′=
.
而∠PBP′=60°,
∴△PBP′是等边三角形,
∴∠2=60°,PP′=BP =
.
∵
,
∴
,∴∠1=90°.
故∠APB=∠1+∠2=150°.
例5、如图,用两个全等的等边三角形△ABC和△ACD拼成菱形叠合,使三角尺的60°角的顶点与点A重合,两边分别与AB、AC重合.将三角尺绕点A按逆时针方向旋转.
① ②
(1)当三角尺的两边分别与菱形的两边BC,CD相交于点E,F时(如图①),通过观察或测量BE,CF的长度,你能得出什么结论?并证明你的结论.
(2)当三角尺的两边分别与菱形的两边BC,CD的延长线相交于点E,F时(如图②),你在(1)中得到的结论还成立吗?简要说明理由.
解:
(1)BE=CF.
∵正△ABC中,∠1+∠2=60°,而∠2+∠3=60°,∴∠1=∠3.
∵正△ABC和正△ACD中AB=AC,∠B =∠4=60°,(视频中90°应为60°)
∴△ABE≌△ACF,∴BE=CF.
(2)(1)中结论仍成立.
∵△ACF可以看作△ABE绕点A逆时针旋转60°得到的.
∴△ABE≌△ACF,∴BE=CF.
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -