1、如图所示,它可以看作是一个__________旋转__________次得到的,每次旋转角为__________;也可以看作是一个__________形旋转__________次得到的,每次旋转角为__________.
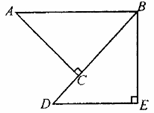
2、如图,△ABC与△BDE是等腰直角三角形,∠ACB=∠E=90°,若△ABC经旋转后能与△BDE重合,那么旋转中心是__________,旋转了__________度.
3、下面有四个图案,它们绕中心旋转一定的角度后,都能和原来的图案相互重合,其中有一个图案与其余三个图案旋转的角度不同,它是__________.(只填序号)

① ② ③ ④
显示答案
|
1、等边三角形;5;60°;有一个角是60°的平行四边;2;120°
2、 点B;45
3、 ① |
4、以图(1)的右边缘所在的直线为轴将该图形向右翻转180°后,再按顺时针方向旋转180°,所得到的图形是( )

图(1) A B C D
5、如图,将左边第一个图案绕中心顺时针旋转,那么旋转180°后得到的图案是( )

6、如图,图案(2)(3)(4)可以看作是由(1)通过旋转得到的,那么图(1)绕其中心旋转( )度得到图案(2)的?( )

A.90° B.180° C.270° D.360°
7、如图,把一个直角三角尺ACB绕30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.

(1)三角尺旋转了多少度?
(2)求∠BDC的度数.
显示答案
|
7、解:(1)∵∠ABC=30°,
∴∠ABE=150°,
∴三角尺绕顶点B旋转了150°.
(2)由旋转知:△ACB≌△EDB,
∴∠ABC=∠DBE=30°,
∴∠CBD=∠ABE=150°,
∵CB=DB,∴∠BDC=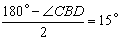 . . |
8、如图所示,已知P为正方形ABCD的对角线AC上一点,(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F.
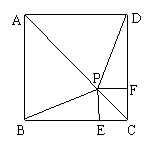
(1)求证:BP=PD;
(2)如图,若四边形PECF绕点C按逆时针方向旋转,在旋转过程中是否总有BP=DP?若是,请给予证明;若不是,请用反例加以说明.
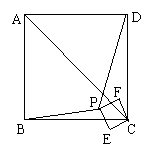
(3)试选取正方形ABCD的两个顶点,分别与四边形PECF的两个顶点连结,使得到的两条线段在四边形PECF绕点C按逆时针方向旋转的过程中长度始终相等,并证明你的结论.
显示答案
|
8、(1)证明△APB≌△APD(SAS)
(2)解:不是总有BP=DP.
理由:若旋转角为45°,
则点P在BC上.
∵正方形ABCD中∠DCP=90°,∴PD>PC.
∵DC=BC,∴PD>BC.
∵BC>PB,∴PD>PB.
(3)解:BE=DF始终成立.
证明:∵正方形ABCD和正方形PECF中,
∠BCD=∠ECF=90°,
∴∠1=∠2.
∵CE=CF,CB=CD,
∴△CBE≌△CDF.
∴BE=DF. |
9、如图,四边形ABCD是正方形,AF平分∠DAG.求证:AG=BG+DF.
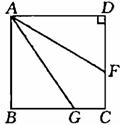
显示答案
|
证明:将△ADF绕点A旋转90°得△ABE,则
∠ABE=∠D=90°,∴∠ABE+∠ABG=180°.
故E、B、G三点共线.
∵∠EAG=90°-∠2=90°-∠1,∠E=∠3=90°-∠1,
∴∠EAG=∠E,∴EG=AG.
又∵BE=DF,
∴AG=EG=EB+BG=DF+BG. |
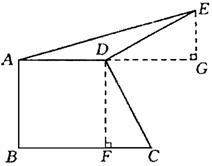
10、如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3.将腰CD以D为中心逆时针旋转90°至DE,连接AE,求△ADE的面积.
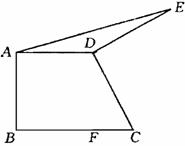
显示答案
|
解:过点D作DF⊥BC,垂足为F.
∵AD=2,BC=3,∴CF=BC-AD=1.
将△DFC绕点D逆时针旋转90°得△DEG,
∴EG=CF=1.
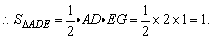
|
|