| 中心对称 |
主编:黄冈中学数学集体备课组
知识点归纳
1.中心对称概念:
①定义:把一个图形绕着某一点旋转180度,如果它能够与另一个图形完全重合,那么就说这两个图形关于这个点中心对称.这个点叫对称中心,这两个图形中的对应点叫做关于中心的对称点;准确把握此定义,要抓住以下三个要素.
(1)有一个对称中心——点;
(2)图形绕中心旋转180°;
(3)旋转后两图形重合.
②中心对称可以看成是旋转变换的特殊情况.
2.中心对称图形的性质:
①关于中心对称的两个图形,对称点所连线段必过对称中心,而且被对称中心平分,
②关于中心对称的两个图形是全等形.
3.轴对称与中心对称对比:
轴对称
中心对称
有一条对称轴——直线
有一个对称中心——点
图形沿对称轴翻转180°后与另一个图形重合
图形绕对称中心旋转180°后与另一个图形重合
典例讲解
例1、填空题
(1)如果△ABC与△EFC关于点C成中心对称,并且A与E是对称点,则四边形ABEF是____________.
(2)如图所示,△ABC与
成中心对称.
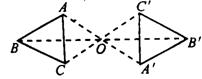
①对称中心是__________,点A的对称点是__________,点B的对称点是__________.
②点A、O、
三点共线吗?__________
③AO=__________,BO=__________,CO=__________.
答案:
(1)平行四边形;
(2)①点O;
;
;②共线;③
;
;
.
例2、选择题
1.下列四组图形中,有几组成中心对称?( )
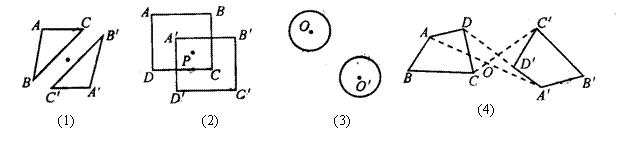
A.1 B.2 C.3 D.4
2.如果两个图形关于某一点成中心对称,那么下列说法正确的个数是( )
①对称点的连线一定经过对称中心
②对应线段一定平行且相等
③将一个图形绕对称中心旋转某个定角必定与另一个图形重合
④一定存在某条直线沿该直线折叠后的两个图形互相重合
A.1个 B.2个 C.3个 D.4个
3.下列图形是由俄罗斯方块拼成的图案,它们之中不成中心对称的是( )
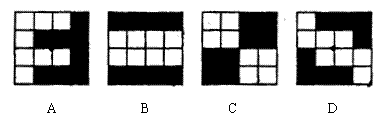
答案:1、C 2、B 3、A
例3、(1)如图,梯形ABCD中,E为CD的中点,请你画出△ADE以点E为对称中心的对称图形.
作法:延长AE、BC交于点
,则△
EC为所求之.
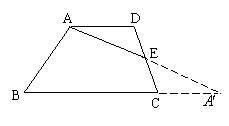
(2)如图,作四边形ABCD以点O为中心的对称图形.

作法:
(1)连接AO,并延长AO到A′,使OA′=OA,则点A、A′关于点O对称;
(2)同法可作点B、C、D关于O的对称点B′、C′、D′;
(3)顺次连接A′、B′、C′、D′所得的四边形A′B′C′D′为所求之.
例4、如图,△
和△ABC关于BC的中点O对称.
求证:AC∥
且AC=
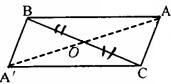
证明:
∵△
和△ABC关于BC的中点O对称,
∴BC、
互相平分于点O,
∴四边形
是平行四边形.
∴AC∥
且AC=
.
例5、如图,△ABC中,AB=AC,E为AB上一点,F是AC的延长线上一点,EF交BC于D.DE=DF,你能判断BE、CF的大小关系吗?请说明理由.
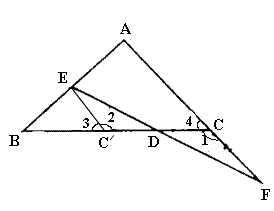
解:
BE=CF.
理由:∵DE=CF ,∴点D是EF的中点.
∴将△DCF绕点D旋转180°到
,
则
,且点C′在BD上,
∴
,
,
∴
∥
,∴∠3=∠4.
∵AB=AC ,∴∠B=∠4,∴∠B=∠3,
∴EB=
,∴BE=CF.
例6、如图,矩形ABCD和矩形
关于点A中心对称.四边形
是菱形吗?为什么?
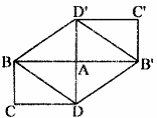
解:
∵矩形ABCD和
关于点A中心对称,
∴
和
互相平分.
∴四边形
是平行四边形.
∵∠BAD=
,∴
⊥
,
∴四边
是菱形.
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -