1、已知,⊙O的半径为3cm,P是⊙O内一点,OP=1cm,则点P到⊙O上各点的最小距离是__________cm,最大距离是__________cm.
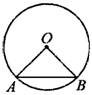
2、如图,已知OA、OB是圆的两条半径,∠OAB=45°,OA=8cm,则AB=__________.
3、如图,在△ABC中,∠ACB=90°,∠A=40°,以C为圆心,CB为半径的圆交AB于点D,则∠ACD=__________.
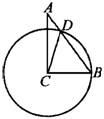
4、如图,△ABC中,∠C=90°,AC=6cm,BC=8cm,分别以A、B为圆心,AC、BC为半径画弧,交斜边于E、F,则EF的长是__________.
显示答案
|
1、2,4
2、
3、10°
4、4cm |
5、平面直角坐标系中有一个点M(2,3),⊙M的半径为r,若⊙M上的点不全在第一象限内,则r的取值范围是( )
A.r=2 B.r=3 C.r≥2 D.r≥3
6、如图,点C在以AB为直径的半圆上,O是圆心,连接OC,则△ABC是( )
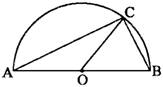
A.锐角三角形 B.钝角三角形
C.直角三角形 D.不能确定
7、如图,点A、D、G、M在半圆O上,四边形ABOC,DEOF,HMNO为矩形,设BC=a,EF=b,NH=c,则下列各式正确的是( )

A.a>b>c B.a=b=c
C.c>a>b D.b>c>a
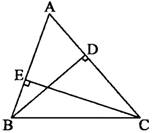
8、如图,BD、CE分别是△ABC的两条高,试说明点E、B、C、D四点在同一个圆上,并画出这个圆.
显示答案
|
解:取BC的中点O,
连接OD、OE.
∵∠BDC=∠BEC=90°
∴OD=OE=OB=OC
∴点E、B、C、D四点在同一圆上. |
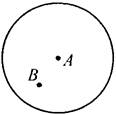
9、如图所示,某部队在灯塔A的周围进行爆破作业,A的周围3千米内的水域为危险区域.有一渔船误入与A距离2千米的B处.为了尽快驶离危险区域,该船应怎样航行?并说明理由.
显示答案
|
解:该船沿AB方向航行最快. 理由:连接AB并延长交⊙A于点C,假设该船不沿BC方向航行而沿任一方向BD航行(点D在⊙A上,不与点C重合).
若点A、B、D不共线,连接AD,则AD=AC
而BA+DB>AD
AC=BC+BA
∴DB>BC
∴不按BC方向航行而按其它任一方向航行离开危险区域圆A的距离都大于BC.
∴该船沿AB方向航行能最快驶离.
|
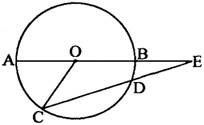
10、如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线相交于点E,已知AB=2DE,∠E=18°,试求∠AOC的度数.
显示答案
|
解:连接OD,则OC=OD,
∴∠C=∠ODC
∵AB是⊙O的直径,
∴AB=2OD
∵AB=2DE
∴OD=DE
∴∠DOB=∠E
∵∠E=18°
∴∠ODC=2∠E=36°
∴∠AOC=∠C+∠E=54°
即∠AOC=54°.
|
|