| 垂直于弦的直径 |
主编:黄冈中学数学集体备课组
知识点归纳
1、圆的对称性:圆是轴对称图形,任一条直径所在的直线都是它的对称轴.
2、垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
3、垂径定理的推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
4、垂径定理的应用:
①用直尺和圆规平分一条弧.作法是过圆心作弧所对弦的垂线,理由是垂径定理;
②在利用垂径定理计算或证明时,我们通常将其化为一个直角三角形的边和角,这个特殊直角三角形的三边分别是半径、弦的一半和圆心到弦的垂线段.
典例讲解
例1、如图,已知以点O为公共圆心的两个同心圆,大圆的弦AD交小圆于B、C.
(1)求证:AB=CD
(2)如果AD=6cm,BC=4cm,求圆环的面积.
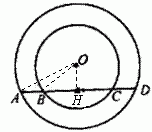
(1) 证明:过点O作OH⊥于点H,
则AH=DH,BH=CH
∴AH-BH=DH-CH
即AB=DC
(2)解:连接OA、OB
由(1)得AH=HD,BH=HC
∴AH=
=3cm,BH=
∴OA2=AH2+OH2=9+OH2,OB2=BH2+OH2=4+OH2
∴OA2-OB2=5(cm2)
故圆环的面积为
例2、如图,AB为⊙O的直径,AB=26cm,CD为⊙O弦,CD=24cm,AB⊥CD于点E,延长CB到点F,使BF=CB,连DF.求DF的长.
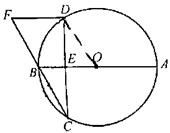
解:
∵AB⊥CD,AB是直径,
∴DE=EC
∵BF=CB,∴BE∥DF,
∴CE=EF
∴DF=2BE
连接OD,则OD=
∵
∴
∵OB=13cm,∴BE=8cm
∴DF=16cm
例3、在直径为10m的圆柱形油槽内装入一些油后,截面如图所示,如果油面宽AB=8m,那么油的最大深度是多少?

解:
过点O作OD⊥AB于点C交
于点D,
则AC=CB.
∴CD的长是油的最大深度,连接OA,则OA=5m
∵AC=
=4cm
∴
∵OD=5m,∴CD=OD-OC=2m
故油的最大深度是2m.
例4、如图,MN为半圆O的直径,半径OA⊥MN,D为OA中点,过D作弦BC∥MN.求证:四边形ABOC为菱形.
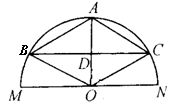
证明:
∵BC∥MN ,OA⊥MN
∴OA⊥BC,∴DB=DC
∵AD=DO
∴四边形ABOC是平行四边形
∴四边形ABOC是菱形
例5、在半径为1的圆中,弦AB、AC分别长
,则∠BAC的度数为多少?
解:
如图过点O作OD⊥AB于点D,OE⊥AC于点E,
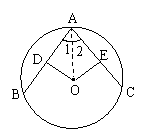
则AD=DB,AE=EC
∴
,AE=
∵AO=1 ,∴
∴
,OE=EA
∴
,
故当AB、AC在点O的两侧时:∠BAC=∠1+∠2=
当AB、AC在点O的同侧时,∠BAC=∠2-∠1=
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -