1、如图,AB是⊙O的弦,圆心O到AB的距离OD=1,AB=4,则该圆的半径是__________.
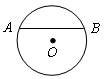
2、如图,水平铺设的圆柱形排水管的截面半径是0.5m,其中水面宽为AB=0.6m,则水的最大深度为__________m.
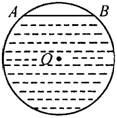
3、如图,点A,B是⊙O上两点,AB=10,点P是⊙O上的动点(P与A,B不重合),连接AP、PB,过点O分别作OE⊥AP于E,OF⊥PB于F,则EF=__________.
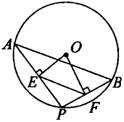
显示答案
|
1、
2、0.9
3、5 |
4、如图,已知AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP∶PB=1∶5,那么⊙O的半径是( )
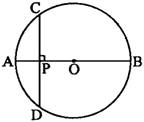

5、圆的半径为13cm,两弦AB∥CD,AB=24cm,CD=10cm,则两弦AB、CD的距离是( )
A.7cm B.17cm C.12cm D.7cm或17cm
6、如图所示,AB是⊙O的一条固定直径,它把⊙O分成上、下两个半圆,自上半圆上一点C作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在上半圆(不包括A、B两点)移动时,点P( )
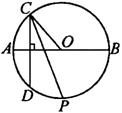
A.到CD的距离保持不变
B.位置不变
C.平分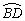
D.随点C的移动而移动
7、“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”此问题的实质就是解决下面的问题:如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,求CD的长.
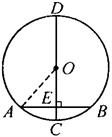
显示答案
|
解:连接OA.
∵OC⊥AB,
∴AE=EB.
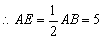 . .
设OE=x,
则OA=OC=x+1,
而OA2-OE2=AE2,
∴(x+1)2-x2=25,
∴x=12.
∴OD=OC=13,
∴CD=OD+OC=26. |
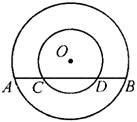
8、H5N1亚型高致病性禽流感是一种传染速度很快的传染病,为防止禽流感蔓延,政府规定:离疫点3千米范围内为扑杀区,所有禽类全部扑杀;离疫点3至5千米范围内为免疫区,所有禽类强制免疫;同时,对扑杀区和免疫区内的村庄,道路实行全封闭管理.现有一条笔直的公路AB通过禽流感疫区,如图所示,O为疫点,在扑杀区内的公路CD长为4千米.问这条公路在免疫区内有多少千米?
显示答案
|
解:过点O作OE⊥CD于点E.连接OA、OC
则CE=ED,AE=EB

设AB=2xkm
则AE=xkm
∵OA=5km,OC=3km
∴OE2=OA2-AE2=25-x2
OE2=OC2-CE2=9-4=5km2
∴25-x2=5
∴x2=20, . . |
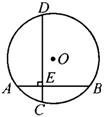
9、如图,⊙O中的弦AB、CD互相垂直于E,AE=5cm,BE=13cm,O到AB的距离为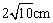 .求⊙O的半径及O到CD的距离. .求⊙O的半径及O到CD的距离.
显示答案
|
解:过点O作OM⊥AB于点M,ON⊥CD于点N.
则四边形OMEN是矩形,∴ON=EM
连接OB,
∵MB=AM
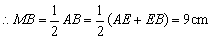
∵BE=13cm
∴ME=BE-BM=4cm
∴ON=4cm
∵在Rt△OMB中,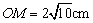 , ,
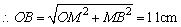 , ,
故⊙O的半径为11cm,O到CD的距离为4cm. |
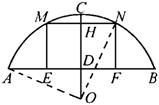
10、如图,某地有一座圆弧形的拱桥,桥下水面宽为7.2m,拱顶高出水面2.4m,现有一艘宽3m,船舱顶部为正方形并高出水面2m的货船要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.
显示答案
|
解:能顺利通过.理由:如图,设圆形拱桥的圆心为点O,过点O作OC⊥AB于点D交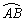 于点C. 于点C.
则AD=DB,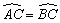
∴CD是拱桥高即CD=2.4m.
又AB=7.2m
∴AD=3.6m
连接OA、ON,
设⊙O的半径为xm,
则OA=OC=ON=xm,
∴OD=(x-2.4)m.
∵Rt△OAD中,
OA2=OD2+AD2
∴x2=(x-2.4)2+3.62
∴x=3.9
∴ON=3.9m,OD=1.5m
∵MN∥AB,∴OH⊥MN
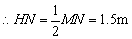
∴Rt△ONH中,
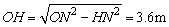
∴DH=OH-OD=2.1m>2m
故此货船能顺利通过. |
|