| 弧、弦、圆心角 |
主编:黄冈中学数学集体备课组
知识点归纳
1. 圆心角:我们把顶点在圆心的角叫做圆心角.
2.圆的特性:①圆是中心对称图形,对称中心是圆心;②把圆绕着它的圆心旋转一个任意角度,都与原来的图形重合,这说明圆具有旋转不变性的特性;
利用以上特性,可以得到以下定理
3.定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
4. 推论:在同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,则它们所对应的其余各组量也相等
典例讲解
例1、如图,已知D、E两点分别为⊙O的半径OA、OB的中点,C为
的中点.求证:CD=CE.
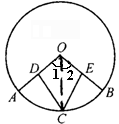
证明:
连接OC ,∵
=
,∴∠1=∠2
∵OD=
,OE=
,OA=OB
∴OD=OE
∵OC=OC
∴△OCD≌△OCE(SAS)
∴CD=CE
例2、如图,AB为⊙O的一条弦,AC=BD,半径OE、OF分别经过点C、D,求证:
.
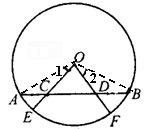
证明:
连接OA、OB
∵OA=OB ,∴∠A=∠B
∵AC=BD ,∴△OAC≌△OBD
∴∠1=∠2,∴
例3、如图,以
的顶点A为圆心,AB为半径作⊙A,交AD、BC于E、F,延长BA交⊙A于G.求证:
.
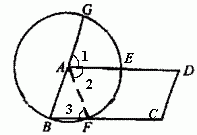
证明:
连接AF.
∵
中,AD∥BC ,∴∠1=∠B ,∠2=∠3
∵AB=AF ,∴∠B=∠3
∴∠1=∠2,∴
例4、如图,已知AB是⊙O的直径,M、N分别是AO、BO的中点,CM⊥AB,DN⊥AB,求证:
.
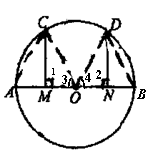
证明:
连接OC、OD,则OC=OD
∵OA=OB ,OM=
,ON=
∴OM=ON
∵∠1=∠2=
∴△OMC≌△OND
∴∠3=∠4 ,∴
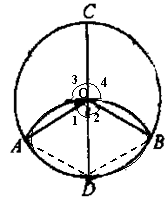
例5、如图,CD为⊙O直径,以D为圆心,DO为半径作弧,交⊙O于两点A、B,连接OA、OB,探究⊙O中
、
、
所对圆心角的大小关系.
解:
、
、
所对圆心角相等
理由如下:
连接AD、DB,则DA=DO
∵OD=OA,∴OA=OD=AD,∴△AOD为正三角形
∴∠1=
. 同理可证∠2=
∵CD为⊙O的直径
∴∠3=
-∠1=
,∠4=
-∠2=
∵∠AOB=∠1+∠2=
∴∠3=∠4=∠AOB
∴
、
、
所对圆心角相等
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -