| 圆周角 |
主编:黄冈中学数学集体备课组
知识点归纳
1.圆周角定义:顶点在圆周上,并且两边都和圆相交的角叫做圆周角.
2.圆周角定理:同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.3.推论:
①同圆或等圆中,相等的圆周角所对的弧一定相等.
②半圆(或直径)所对圆周角是直角,90°的圆周角所对的弦是直径.
③如果三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形.
4.圆的内接四边形:
①定义:如果一个多边形的所有顶点都在同一圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
②圆内接四边形的性质:圆内接四边形的对角互补.
典例讲解
例1、如图,AB=AC,E、F分别在
上,若∠ABC=
,求:∠BEC和∠BFC的度数.

解:
∵AB=AC ,∠ABC=
,
∴∠A=
,
∴
.
∵∠BFC+∠BEC=
,
∴∠BFC=
.
例2、如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交BC于D.若BC=8,ED=2,求⊙O的半径.

解:
∵OD⊥BC,∴BE=EC,
∵O是直径AB的中点,
∴AC=2OE,设⊙O的半径为x,
则AB=2x,OE=x-2,AC=2(x-2),
∵∠C=90°,∴AC2+BC2=AB2,
∴4(x-2)2+64=4x2,
∴x=5.⊙O的半径为5.
例3 如图,已知BC为半圆O的直径,AB=AF,AC交BF于点M,过A作AD⊥BC于D,交BF于E,则AE与BE的大小有什么关系?为什么?
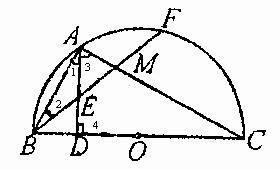
解:
AE=BE.理由:
∵BC是半⊙O的直径
∴∠1+∠3=
∵∠4=
,
∴∠3+∠C=
,
∴∠1=∠C
∵AB=AF
∴∠2=∠C.
∴∠1=∠2.
∴AE=BE.
例4 如图,已知⊙O的直径AB和弦CD,AB⊥CD于E,F为DC延长线上一点,连结AF,交⊙O于M点.求证:∠AMD=∠FMC.
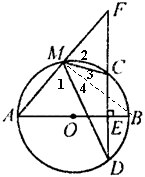
证明:
连接MB.
∵AB是⊙O的直径,
∴∠AMB=90°
即∠1+∠4=∠2+∠3=90°
∵OB⊥CD
∴∠3=∠4
∴∠1=∠2
即∠AMD=∠FMC.
例5、如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,作∠BAC的外角平分线AE交⊙O于点E,连接DE.求证:DE=AB.
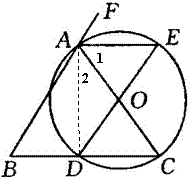
证明:
连接AD,
∵AC是⊙O的直径,∴∠ADC=90°,即AD⊥BC
∵AB=AC,∴AD平分∠BAC,
∴∠2=
∠BAC,
∵AE平分∠CAF,∴∠1=
∠CAF,
∵∠BAC+∠CAF=180°
∴∠1+∠2=90°,
∴DE是⊙O的直径
∴AC=DE
于是DE=AB
此题也可以运用角的代换,证明四边形ABDE为平行四边形得到DE=AB.
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -