1、如图,A、B、C是⊙O上三点,∠ACB=40°,则∠ABO等于__________度.
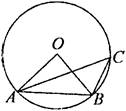
2、如图,△ABC的顶点都在⊙O上,∠C=30°,AB=2cm,则⊙O的半径为__________cm.
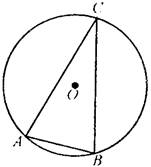
3、如图,在平面直角坐标系中,P是经过O(0,0),A(0,2),B(2,0)的圆上的一个动点(P与O、A、B不重合),则∠OAB=__________,∠OPB=__________.
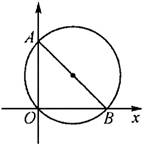
4、如图,△ABC内接于⊙O,∠B=∠OAC,OA=8cm,则AC=__________cm.
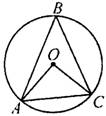
5、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则BC=__________.

显示答案
|
1、50
2、2
3、45°;45°或135°
4、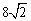
5、6 |
6、如图,BD是⊙O的直径,弦AC、BD相交于点E,则下列结论不成立的是( )
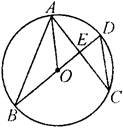
A.∠ABD=∠ACD B.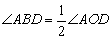
C.∠BAE=∠BDC D.∠ABD=∠BDC
7、如图,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于( )

A.80° B.50°
C.40° D.20°
8、如图,AB为⊙O的直径,BD是⊙O的弦,延长到C,使BD=DC,连接AC交⊙O于点F,点F不与点A重合.
(1)AB与AC的大小有什么关系?为什么?
(2)按角的大小分类,请你判断△ABC属于哪一类三角形,并说明理由.
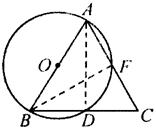
显示答案
|
解:(1)AB=AC.
理由:连接AD
∵AB是⊙O的直径
∴∠ADB=90°,即AD⊥BC
∵BD=DC
∴AB=AC
(2)△ABC属于锐角三角形.
理由:连接BF
∵点A、F不重合,
AB是⊙O的直径. |
9、如图,△ABC的三个顶点都在⊙O上,CN为⊙O的直径,CM⊥AB,交⊙O于M,点F为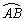 的中点. 的中点.
求证:(1) ; ;
(2)CF平分∠NCM.

显示答案
|
证法一:(1)连接OF.
∵点F为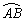 的中点 的中点
∴OF⊥AB
∵CM⊥AB
∴CM∥OF
∴∠1=∠F
∵OC=OF
∴∠2=∠F
∴∠1=∠2
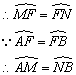
(2)∵∠1=∠2
∴CF平分∠NCM.
证法二
(1)连接BN
∵CN是⊙O的直径,
∴∠CBN=90°
∴∠N+∠5=90°
∵∠3=90°
∴∠4+∠A=90°
∵∠A=∠N
∴∠4=∠5
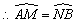
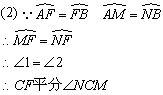 |
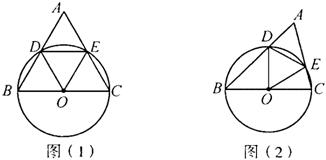
10、如图(1),已知△ABC是等边三角形,以BC为直径的⊙O交AB、AC于D、E.
(1)求证:△DOE是等边三角形;
(2)如图(2),若∠A=60°,AB≠AC,则(1)的结论是否成立?如果成立,请给出证明,如果不成立,请说明理由.
显示答案
|
解:(1)∵△ABC是等边三角形,∴∠B=60°,
∵OB=OD,∴∠ODB=60°,∴∠DOB=60°,
同理∠COE=60°,∴∠DOE=60°,
∵OD=OE,∴△DOE是等边三角形
(2)结论仍成立。∠B+∠C=120°,∴∠ODB+∠OEC=120°,
∴∠DOB+∠COE=360°-120°-120°=120°
∴∠DOE=60°,∵OD=OE,
∴△DOE是等边三角形. |
|