课外拓展 |
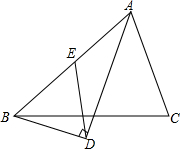
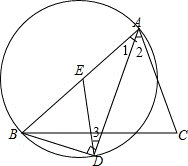
例、已知:如图,在△ABC中,点D是∠BAC的角平分线上一点,BD⊥AD于点D,过点D作DE∥AC交AB于点E.求证:点E是过A,B,D三点的圆的圆心.
分析: 要求证:点E是过A,B,D三点的圆的圆心,只要证明AE=BE=DE即可,可以根据等角对等边可以证得. 证明:∵点D在∠BAC的平分线上, ∴∠1=∠2.
又∵DE∥AC, ∴∠2=∠3, ∴∠1=∠3. ∴AE=DE. 又∵BD⊥AD于点D, ∴∠ADB=90°. ∴∠EBD+∠1=∠EDB+∠3=90°. ∴∠EBD=∠EDB. ∴BE=DE. ∴AE=BE=DE. ∵过A,B,D三点确定一圆,又∠ADB=90°, ∴AB是A,B,D所在的圆的直径. ∴点E是A,B,D所在的圆的圆心.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||