| 直线和圆的位置关系(1) |
主编:黄冈中学数学集体备课组
知识点归纳
1.直线和圆的位置关系:
①相交:直线和圆有两个公共点,这时说这条直线和圆相交;这条直线叫做圆的割线;
②相切:直线和圆有唯一公共点,这时说这条直线和圆相切;这条直线叫做圆的切线,这个点叫做切点.
③相离:直线和圆没有公共点,这时说这条直线和圆相离.
2.直线和圆的位置关系的判定:
(1)定理:若⊙O的半径为R,圆心到直线l的距离为d. 则
直线l与⊙O相交
d﹤R;
直线l与⊙O相切
d =R;
直线l与⊙O相离
d﹥R;
(2)“圆心到直线的距离d和半径R的数量关系”与“直线和圆的位置关系”之间的对应与等价关系列表如下:
直线与圆的位置关系
相交
相切
相离
公共点个数
2个
1个
0个
d与R的关系
d<R
d=R
d>R
典例讲解
例1、填空题
1.在Rt△ABC中,∠C=
,AC=3cm,AB=6cm,以点C为圆心,与AB边相切的圆的半径为_________cm.
2.如图,⊙O的半径OD为5cm,直线l⊥OD,垂足为O,则直线l沿射线OD方向平移_________cm时与⊙O相切.

3.已知⊙O的直径为6cm,如果直线l上的一点C到圆心的距离为3cm,则直线l与⊙O的位置关系是_________.
4.⊙O的半径为R,圆心O到直线l的距离d与R是方程x2-6x+9=0的两个实数根,则直线l和⊙O的位置关系是_________.
答案:1.
2. 5 3. 相切或相交 4. 相切
例2、如图,△ABC中,AB=4,∠C=
,∠B=
,AO=x,O在AB边上,且⊙O的半径为1,问当x在什么范围内取何值时,AC与⊙O相离、相切、相交?
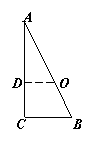
解:
过点O作OD⊥AC于点D,则OD=
∴当OD<1即x<2时直线AC与⊙O相交,
当OD=1即x=2时,直线AB与⊙O相切,
当OD>1,即2<x≤4时,AC与⊙O相离.
例3、如图,在△ABC中,E、F分别是AC、BC的中点,CD⊥AB于D,垂足为D,且CD=EF,求证:以EF为直径的圆与AB相切.

证明:
取EF的中点O,过点O作OH⊥AB于点H,
设CD交EF于点G,则点O为以EF为直径的圆的圆心.
∵E、F分别是CA、CB的中点,
∴EF∥AB ,∴CG=GD ,∴GD=
.
∵CD⊥AB ,∴OH=GD.
∵CD=EF ,∴OH=
.
故以EF为直径的圆与AB相切.
例4、如图,公路MN和公路PQ分别在P点处交汇,且∠QPN=
,点A处有一所中学,AP=160m,假设拖拉机行驶时,周围100m内会受到噪音的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到噪声的影响?请说明理由.如果受影响,当拖拉机的速度为18km/h时,学校受影响的时间为多少秒?

解:
受影响,理由:
过点A作AB⊥MN于点B,
∵∠1=
, ∴
.
∴受影响;以点A为圆心,100m为半径画圆交MP于点C1、C2,连接AC1、AC2,则拖拉机由C1行驶到C2时,学校受影响.
∵AC1=AC2=100m,∴C1C2=2BC1 .
∴
,∴C1C2=120m.
故学校受影响的时间为(
)×3600=24(s).
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -