| 直线和圆的位置关系(2) |
主编:黄冈中学数学集体备课组
知识点归纳
1.切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线;
①分析切线的判定定理与前一节课所学习的定理比较,切线的判定定理是由圆心到直线的距离等于半径所得到的;
②在判断一条直线是圆的切线时,一般有两种类型:一种是直线经过圆上一点,具体方法是连接这一点和圆心;另一种是不知道直线是否经过圆上一点,具体方法是,过圆心作直线的垂线,证明垂线段等于半径.
2.切线的性质:
①定理的内容是切线垂直于过切点的半径;
②切线和圆心的距离等于半径;
③经过圆心且垂直于切线的直线必过切点;
④经过切点垂直于切线的直线必过圆心.
综上所述,在解决有关圆的切线的问题,连接圆心和切点的线段是最常见的辅助线.
典例讲解
例1、如图,已知等腰△ABC中,点O在BC上,以点O为圆心作圆,分别切两腰于D、E两点,AB=10cm,BC=12cm.求⊙O的半径.
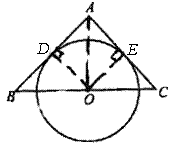
解:
连结OD、OE、OA,则OD=OE.
∵AB切⊙O于点D , ∴OD⊥AB.
∵AC切⊙O于点E , ∴OE⊥AC.
∴AO平分∠BAC ,
∵AB=AC=10cm,∴∠B=∠C.
∵OD=OE,∴△OBD≌△OCE,
∴BO=OC ,即OB=
BC=6cm.
∵AO⊥BC
∴
∵
∴
=4.8cm
故⊙O的半径为4.8cm.
例2、如图,AB是⊙O的直径,BC切⊙O于点B,AD∥CO.求证:CD是⊙O的切线.
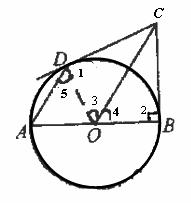
证明:
连接OD.
∵AD∥CO,∴∠3 =∠5,∠A=∠4,
∵OA=OD,∴∠A=∠5.
∴∠4=∠3.
∵OD=OB,OC=OC,
∴△OCD≌△OCB, ∴∠1=∠2.
∵BC切⊙O于点B,
∴∠2=
,∴∠1=
,
∴OD⊥CD.
∵OD是⊙O的半径,
∴DC是⊙O的切线.
例3、在图1和图2中,已知OA=OB,AB=24,⊙O的直径为10.
(1)如图1,若AB与⊙O相切于点C,试求OA的值.
(2)如图2,若AB与⊙O相交于D、E两点,且D、E均为AB的三等分点,试求OA的值.
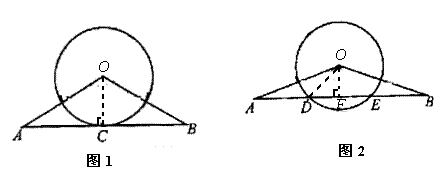
解:
(1)连接OC
∵AB与⊙O相交于点C
∴OC⊥AB ,∵OA=OB
∴AC=CB,即AC=
AB=12
∵OC=5 ,∴
(2)过点O作OF⊥AB于点F,则DF=FE=4.
连接OD,则OD=5,
∵DE=
=8,∴DF=
DE=4,
∴
,AF=AO+DF=12,
∴
.
例4、如图,已知等边△ABC,以边BC为直径的半圆与边AB、AC分别交于点D、点E,过点D作DF⊥AC,垂足为点F.
(1)判断DF与⊙O的位置关系,并证明你的结论.
(2)过点F作FH⊥BC、垂足为点H.若等边△ABC的边长为4.求FH的长.(结果保留根号)
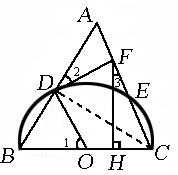
解:
(1)DF与⊙O相切,连接OD,则OD=OB.
∵等边△ABC中,∠C=
,∠B=
,
∴△OBD是正三角形,
∴∠1=∠C=
.
∴OD∥AC,
∵DF⊥AC,∴DF⊥OD
∵OD是⊙O的半径,∴DF与⊙O相切.
(2)连接DC.∵BC是⊙O的直径,
∴∠BDC=
.
∵正△ABC中,CA=CB=4,
∴AD=DB ,即
.
∵∠A=
,∠AFD=90°,
∴∠2=
,AF=
AD=1,∴FC=AC-AF=3.
∵∠FHC=
,∠ACB=
,∴∠3=30°,
∴HC=
FC=
,∴FH=
.
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -