例、（武汉）如图，已知：在直角坐标系中．点E从O点出发，以1个单位/秒的速度沿x轴正方向运动，点F从O点出发，以2个单位/秒的速度沿y轴正方向运动．B（4，2），以BE为直径作⊙O1．
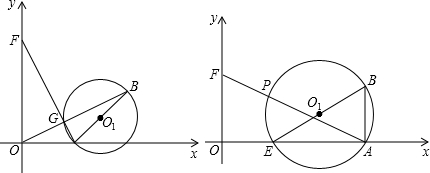
（1）若点E、F同时出发，设线段EF与线段OB交于点G，试判断点G与⊙O1的位置关系，并证明你的结论；
（2）在（1）的条件下，连接FB，几秒时FB与⊙O1相切？
（3）若点E提前2秒出发，点F再出发．当点F出发后，点E在A点的左侧时，设BA⊥x轴于点A，连接AF交⊙O1于点P，试问AP·AF的值是否会发生变化？若不变，请说明理由并求其值；若变化，请求其值的变化范围．
分析：
（1）要判断点G与⊙O1的位置关系，只需比较O1G与⊙O1的半径O1B的大小．设点E出发t秒，则E（t，0），F（0，2t），用待定系数法求出直线EF和直线OB的解析式，确定点G的坐标，用勾股定理计算出O1G与O1B的大小，从而进行判定．
（2）如果t秒时FB与⊙O1相切，那么∠FBE=90°；在RT△BEF与RT△OEF中，根据EF不变列出方程，求出t的值．
（3）设点F出发t秒，则E（t+2，0），F（0，2t）；设P（x，y），由y：（4-x）=2t：4，得出x=
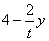，即P（
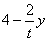，y）；因为BE为直径，所以∠BPE=90°，PE2+BP2=BE2，得出y与t的关系，可以含t的代数式得出P的坐标，分别计算AP，AF的长，根据结果判断．
解：（1）设点E出发t秒，则E（t，0），F（0，2t）；
设直线EF的方程为y=kx+b，则
，
∴解得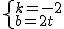
，
∴y=-2x+2t，
∴直线OB的方程为
；
∵解方程组
，
得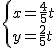
，
∴G（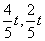
）；
∵O1是BE的中点，
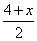∴O1（
，1），
∴
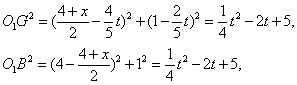
∴O1G=O1B，点G在⊙O1上．
（2）设t秒时FB与⊙O1相切，那么E（t，0），F（0，2t），∠FBE=90°；
∵EF2=BE2+BF2，EF2=OE2+OF2，
∴（4-t）2+22+42+（2-2t）2=t2+（2t）2，
解得t=2.5．
（3）设点F出发t秒，则E（t+2，0），F（0，2t），
设P（x，y）；
∵y∶（4-x）=2t∶4，
∴
，
∴P（
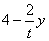，y）．
∵BE为直径，
∴∠BPE=90°．
∵PE2＋BP2=BE2
∴
，
∴
，
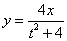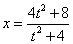即P（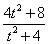
，
），
∴
，
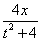∴AP=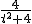
×
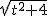，AF=
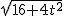=2．
∴AP·AF=8，是不会发生变化的．
点评：
本题综合考查了切线的判定，三角函数等知识，解题中要善于抓住不变量，找到等量关系，题目有一定难度，可以考查学生的综合实力．
