1、下列说法正确的是( )
A.垂直于切线的直线必过切点
B.垂直于半径的直线是圆的切线
C.圆的切线垂直于经过切点的半径
D.垂直于切线的直线必经过圆心
2、已知Rt△ABC的直角边AC=BC=4cm,若以C为圆心,以3cm的长为半径作圆,则这个圆与斜边所在的直线的位置关系是( )
A.相交 B.相切
C.相离 D.不能确定
3、如图,在△ABC中,AB=2,AC=1,以AB为直径的圆与AC相切,与边BC交于点D,则AD的长为( )
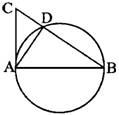

4、如图,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=25°,∠D=__________.
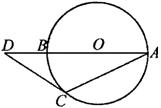
5、如图,⊙O的半径为1,圆心O在正三角形的边AB上沿图示方向移动,当⊙O移动到与AC相切时,OA=__________.
显示答案
|
4、40°
5、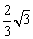 |
6、如图,以边长为4的正△ABC的BC边为直径作⊙O与AB相交于点D,⊙O的切线DE交AC于E,EF⊥BC,点F是垂足,求EF的长.
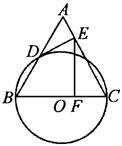
显示答案
解析:连接CD,则BD=AD=2,∠ADE=30°,所以AE= AD=1,EC=4-1=3,∠CEF=30°,FC= AD=1,EC=4-1=3,∠CEF=30°,FC= EC= EC=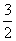 ,所以EF= ,所以EF= . . |
7、已知:△ABC内接于⊙O,过点A作直线EF.
(1)如图1,AB为直径,要使得EF是⊙O的切线,还需添加的条件是(只写出三种):
①__________或②__________或③__________.
(2)如图2,AB为非直径的弦,且∠CAE=∠B.求证:EF是⊙O的切线.
显示答案
|
解:(1)①OA⊥EF ②∠CAE=∠B ③∠FAB=∠C ④∠EAB=∠C
(2)证明:作⊙O的直径AD,连接CD.
∠ACD=90°
∴∠D+∠CAD=90°
∵∠D=∠B,∠CAE=∠B
∴∠CAE =∠D
∴∠CAE+∠CAD=90°
即∠EAD=90°
∴AD⊥EF
∴EF是⊙O的切线. |
8、如图,PA是⊙O的切线,切点是A,过点A作AH⊥OP于点H,交⊙O于点B.求证:PB是⊙O的切线.
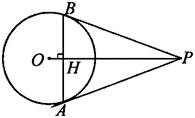
显示答案
|
证明:连接OA、OB.
∵OA=OB,AH⊥OP
∴AH=HB
∴PA=PB
∴∠PBA=∠PAB
∵∠OBA=∠OAB
∴∠OBP=∠OAP=90°
∴PB是⊙O的切线 |
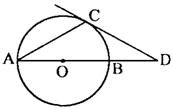
9、如图,已知AB是⊙O的直径,AB=2,∠BAC=30°,点C在⊙O上,过点C与⊙O相切的直线交AB的延长线于点D,求线段BD的长.
显示答案
|
解:连接OC.
∵OC=OA,∠A=30°
∴∠COD=2∠A=60°
∵DC切⊙O于点C
∴∠OCD=90°
∴∠D=30°
∵⊙O的直径AB=2
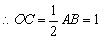
∴OD=2OC=2
∵OB=1
∴BD=OD-OB=1. |
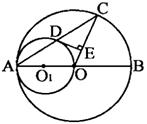
10、如图,AB是⊙O的直径,以OA为直径的⊙O1与⊙O的弦AC相交于点D,DE⊥OC,垂足为E.求证:DE是⊙O1的切线.
显示答案
|
证明:连接O1D,OD
∵AO是⊙O1的直径
∴∠ADO=90°,
即OD⊥AC
∴AD=DC
∴AO1=O1O
∵DE⊥OC
∴DE⊥O1D
∵O1D是⊙O1的半径
∴DE是⊙O1的切线. |
|