初中和高中九科名师视频课程免费试听1200分钟
高一课程	高一全科强化班辅导课程  免费听课	初一课程	初一全科强化班辅导课程  免费听课
高二课程	高二全科强化班辅导课程  免费听课	初二课程	初二全科强化班辅导课程  免费听课
高三课程	高三全科全年强化班课程  免费听课	初三课程	初三中考双重强化班课程  免费听课
直播讲座	初中高中名师免费公开课  免费听课	小学课程	小学全科全年强化班课程  免费听课

例、如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=24cm，BC=26cm，AB为⊙O的直径，动点P从点A开始沿AD边向点D以1cm/s的速度运动，动点Q从点C开始沿CB边向点B以3cm/s的速度运动．P、Q分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t(s)．求：

　　(1)t分别为何值时，四边形PQCD为平行四边形、等腰梯形？

　　(2)t分别为何值时，直线PQ与⊙O相切、相交、相离？

解：

　　(1)∵AD∥BC，∴当PD=CQ时，四边形PQCD是平行四边形．

　　∵PD=24－t，CQ=3t，∴24－t=3t，∴t=6．

　　当PQ=CD，PQ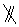CD时，四边形PQCD是等腰梯形．

　　过P作PE⊥BC于E，过D作DF⊥BC于F，则四边形PEFD均为矩形．△PQE≌△DCF．

　　∴PD=EF=(24－t)cm，QE=FC=26－24=2(cm)，QC=3tcm．

　　又∵QE＋FC=QC－PD，∴2＋2=3t－(24－t)，∴t=7．

　　故，当t=6s时，四边形PQCD为平行四边形；当t=7s时，四边形PQCD是等腰梯形．

　　(2)设运动ts时，直线PQ与⊙O相切于点G．

　　过P作PH⊥BC于H，即PH=AB=8，BH=AP，HQ=26－3t－t=26－4t，PQ=AP＋BQ=26－2t．

　　由PQ2=PH2＋HQ2，得(26－2t)2=82＋(26－4t)2．

　　解得．故当或t=8s时，直线PQ与⊙O相切；

　　当或时，直线PQ与⊙O相交；

　　当时，直线PQ与⊙O相离．

初中和高中九科名师视频课程免费试听20小时
年级	课程名称	免费听课	课程详情
高一课程	高一全科点睛班课程	免费听课	查看详情>>
	高一全科强化班课程	免费听课	查看详情>>
高二课程	高二全科全年强化班	免费听课	查看详情>>
高三课程	高三全科强化班课程	免费听课	查看详情>>
初一课程	初一全科强化班课程	免费听课	查看详情>>
	初一全科点睛班课程	免费听课	查看详情>>
初二课程	初二全科强化班视频	免费听课	查看详情>>
	初二全科点睛班课程	免费听课	查看详情>>
初三课程	初三全科强化班	免费听课	查看详情>>
	全科巨无霸同步提高课程	免费听课	查看详情>>
小学课程	小学全年全科强化班	免费听课	查看详情>>
	更多课程+更多介绍>>点击进入

 

 

-END-