证明：∵E是△ABC的内心，
∴∠4=∠5，∠2=∠3．
又∵∠1=∠5，∴∠1=∠4．
又∵∠DBE=∠1＋∠2，∠DEB=∠3＋∠4，
∴∠EBD=∠DEB．
∴DE=BD．
点评：
这里是充分运用内心的定义，找出相等的角，∠BED是一个与圆无关的角，一般运用外角进行转化．
例2、(沈阳市)如图(1)，直线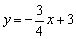
与x轴相交于点A，与y轴相交于点B，点C(m,n)是第二象限内任意一点，以点C为圆心的圆与x轴相切于点E，与直线AB相切于点F．
(1)当四边形OBCE是矩形时，求点C的坐标；
(2)如图(2)，若⊙C与y轴相切于点D，求⊙C的半径r；
(3)在⊙C的移动过程中，能否使△OEF是等边三角形(只回答“能”或“不能”)？
解：
(1)如图(1)，当x=0时，y=3；当y=0时，x=4．∴A(4,0)，B(0,3)．
∴OA=4，OB=3，AB=5．
连结CF、CB、CE．
当四边形OBCE为矩形时，有CF=CE=OB=3，
故CB∥x轴．
∴∠CBF=∠BAO．
∵⊙C与直线AB相切于点F，∴CF⊥AB于点F．
∴∠CFB=∠BOA．又∵CF=OB，
∴△CBF≌△BAO．
∴CB=AB=5，∴点C的坐标为(－5,3)．
(2)如图(2)，连结CE、CF、CD．
∵⊙C与x轴、y轴、AB分别相切于点E、D、F，
∴由切线长定理得AF=AE，BF=BD，OE=OD，
∴
．
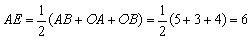由切线性质定理得，CE⊥x轴于点E，CD⊥y轴于点D，
∴四边形CEOD为矩形．又∵CE=CD，
∴四边形CEOD为正方形．∴OE=CE=r．
∵OE=AE－OA=6－4=2，
∴⊙C的半径为2．
