| 圆和圆的位置关系 |
主编:黄冈中学数学集体备课组
知识点归纳
1、两圆的位置关系:

(1)两圆外离:两个圆没有公共点,并且每个圆上的点都在另一个圆的外部(如图 (1)).
(2)两圆外切:两个圆有唯一的公共点,并且除了这个公共点以外,每个圆上的其余点都在另一个圆的外部(如图 (2)).
(3)两圆相交:两个圆有两个公共点(如图 (3)).
(4)两圆内切:两个圆有唯一的公共点,并且除了这个公共点以外,其中一个圆上其余的点都在另一个圆的内部(如图 (4)).
(5)两圆内含:两个圆没有公共点,并且一个圆上的点都在另一个圆的内部,两圆同心是两圆内含的一种特例(如图 (5)).
外离和内含统称两个圆相离,外切与内切统称两个圆相切.这样,两个圆的位置关系可分为三大类,即相离、相切、相交.
2、两圆的位置关系的定理:
如果两圆的半径分别为R和r(R>r),圆心距(两圆圆心的距离)为d,则

另外,我们可以用数轴来反映两圆的位置与两圆半径、圆心距之间的数量关系(如图).

3、常用辅助线:
作相切两圆连心线,作相交两圆公共弦.
典例讲解
例1、已知⊙A、⊙B、⊙C两两外切,它们的圆心距分别是AB=8cm,BC=13cm,CA=11cm,求这三个圆的半径.
解:
设⊙A、⊙B、⊙C的半径分别为 xcm,ycm,zcm,
则
,解得
故⊙A的半径为3cm,⊙B的半径为5cm,⊙C的半径为8cm.
例2、如图:
与
外切于点P,过点P的直线交
于点A,交
于点B,求证:
∥
.
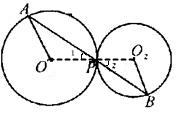
证明:
连接
、
、
.
∵
与
外切于点P,∴
=
+
∴
、P、O2三点共线,∴∠1=∠2.
∵
=
,∴∠A=∠1.
∵
=
,∴∠2=∠B,
∴∠A=∠B,∴
∥
.
例3、如图,已知两个等圆
和
相交于A、B两点,
经过点
,求∠
的度数.
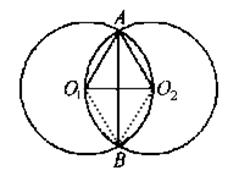
解:
∵两个等圆
、
相交于点A、B ,
∴
=
.
∵
经过点O2,∴
=
,
∴△
是正三角形, ∴∠
=
.
连接
、
,则
=
=
=
,
∴四边形AO1BO2是菱形,
∴
.
例4、如图,施工工地的水平地面上,有三根外径都是1米的水泥管,两两相切地堆放在一起,则其最高点到地面的距离是多少?
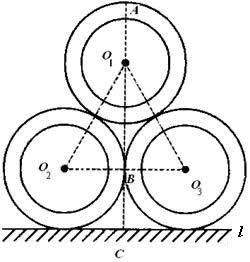
解:
如图,连接O1O2,O2O3,O3O1,过点O1作AC⊥l于点C,交O2O3于点B,交
于点A,则AC的长为所求之.
∵直径为1m的三个圆两两外切,
∴O1O2=O2O3=O1O3=1m ,显然O2O3∥l,
∴O1C⊥O2O3,∴O2B=BO3,即
∴
显然
,∴
.
故其最高点到地面的距离是
.
高一全科点睛班课程 高一全科强化班课程 高二全科全年强化班 高三全科强化班课程 初一全科强化班课程 初一全科点睛班课程 初二全科强化班视频 初二全科点睛班课程 初三全科强化班 全科巨无霸同步提高课程 小学全年全科强化班
- 返回 -