|
一、选择题
1、设⊙O1,⊙O2的半径分别是3,2,给出以下命题:①当O1O2=1时,⊙O1与⊙O2内切;②当O1O2=3时,⊙O1与⊙O2相交;③当O1O2=5时,⊙O1与⊙O2外切;④当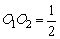 时,⊙O1与⊙O2内含;⑤当O1O2=7时,⊙O1与⊙O2外离.其中正确的有( ) 时,⊙O1与⊙O2内含;⑤当O1O2=7时,⊙O1与⊙O2外离.其中正确的有( )
A.2个 B.3个
C.4个 D.5个
2、两圆相切,半径分别为4cm和9cm,则两圆的圆心距是( )
A.5cm B.13cm
C.5cm或13cm D.2.5cm或6.5cm
3、已知⊙O的半径为6cm,P是⊙O外一点,且OP=10cm,以P为圆心的圆与⊙O相切时,⊙P的半径为( )
A.4cm B.16cm
C.4cm或16cm D.2cm或8cm
二、填空题
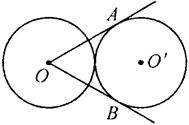
4、如图,两个等圆⊙O和⊙O′外切,过O点作⊙O′的两条切线OA、OB,A、B为切点,则∠AOB=_________.
5、两圆的半径之比是5:3,外切时圆心距是32,那么当这两个圆内切时,圆心距为_________.
6、如图,用半径R=3cm,r=2cm的钢球测量口小内大的内孔的直径D,测得钢球顶点与孔口平面的距离分别为a=4cm,b=2cm,则内孔直径D的大小为_________.

显示答案
|
4、60°
5、8
提示:设两圆的半径为5x,3x,则5x+3x=32,解得x=4.当两圆内切时,圆心距为5x-3x=2x=8.
6、9cm |
三、解答题
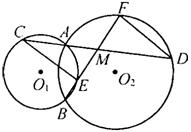
7、如图,⊙O1和⊙O2相交于点A、B,过点A的直线分别交两圆于C、D,M是CD的中点,直线BM分别交两圆于点E、F.
(1)求证:CE∥DF;
(2)求证:ME=MF.
显示答案
|
证明:(1)连接AB.
则∠D=∠B,∠C=∠B.
∴∠D=∠C
∴CE∥DF
(2)∵∠CME=∠DMF,
MC=MD
∠C=∠D
∴△MCE≌△MDF
∴ME=MF. |
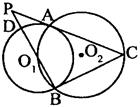
8、如图,⊙O1与⊙O2相交于A、B两点,O1在⊙O2上,⊙O2的弦BC切⊙O1于B,延长BO1、CA交于点P,PB与⊙O1交于点D.
(1)求证:AC是⊙O1的切线;
(2)连接AD、O1C,求证:AD∥O1C.
显示答案
|
证明:(1)连接O1A、O1C
∵BC切⊙O1于点B
∴O1B⊥BC
∴∠B=90°
∴O1C是⊙O2的直径
∴∠O1AC=90°
∴O1A⊥AC
∵O1A是⊙O1的半径
∴AC是⊙O1的切线
(2)连接AB
∵CA、CB切⊙O1于点A、B
∴CA=CB,CO1平分∠ACB
∴O1C⊥AB
∵BD是⊙O1的直径
∴AD⊥AB
∴AD∥O1C. |
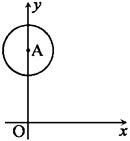
9、如图,已知A点坐标为(0,3),⊙A的半径为1,点B在x轴上.
(1)若点B坐标为(4,0),⊙B的半径为3,试判断⊙A与⊙B的位置关系;
(2)若⊙B过点M(2,0),且与⊙A相切,求B点坐标.
显示答案
|
解:(1)∵B(4,0),A(0,3)
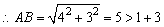
∴⊙A与⊙B外离
(2)设点B的坐标为(x,0)
①当⊙B与⊙A外切时,点B必在点M的左侧,而M(2,0)
于是BM=2-x
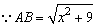
AB=BM+1
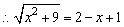
∴x=0,∴B(0,0)
②当⊙B与⊙A内切时
BM>1且点B必在点M的左侧,
于是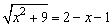
∴x=-4,∴B(-4,0) |
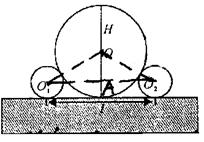
10.有一巨型广告牌,如图所示,形状为圆形(如⊙O所示),顶端不易到达,为了测量此广告牌的高度H,有人建议:用两个半径r为0.5米的等圆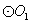 和 和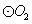 如图所示放置,此时,只需测量出l的长,即可求出广告牌的高度. 如图所示放置,此时,只需测量出l的长,即可求出广告牌的高度.
(1)如果测量出l的长为8米,请你帮忙计算出广告牌的高度H;
(2)试推导广告牌的高度H与l之间的关系式.
显示答案
|
解:(1)设⊙O与地面相切于点B,连接OO1、OO2、O1O2交OB于点A,则:
AB=0.5m,H=2OB,O1O2=l,
显然OB⊥O1O2,设⊙O的半径为xm,则OA=(x-0.5)m,OO2=OO1=(x+0.5)m,
∴O1A=O2A ,即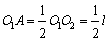 . .
∵ , ,
∴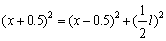 ,∴ ,∴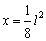 ,即 ,即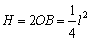 . .
故如果测量出l的长为8m,则广告牌的高H为16m.
(2)广告牌的高度H与l之间的关系为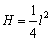 . . |
|