| 正多边形和圆 |
主编:黄冈中学数学集体备课组
知识点归纳
1. 正多边形
①定义:各边相等,各角也相等的多边形,叫做正多边形;
②定义中两个条件缺一不可.
我们知道三边相等的三角形是正三角形,三个角相等的三角形也是正三角形.但菱形四条边相等,却不是正四边形.矩形四角都相等,也不是正四边形.所以正多边形的定义中各边相等和各角相等两个条件缺一不可.
2. 正多边形与圆的关系
把一个圆分成相等的一些弧,就可以得到这个圆的内接正多边形,这个圆是这个多边形的外接圆.
3、正多边形中各元素间的关系
一个正多边形的外接圆的圆心叫做这个正多边形的中心.外接圆的半径叫做正多边形的半径.正多边形每一边所对的圆心角叫做正多边形的中心角.中心到正多边形的一边的距离叫做正多边形的边心距.如图,设正多边形的边长为an,半径为R,边心距为rn,中心角为αn,则它们有如下关系:
;

正n边形的中心角
;(视频中应为
)
正n边形的周长Pn=nan;
正n边形的面积
.
4、正多边形有关计算
在解决有关正多边形计算时,通常运用转化的思想方法,将正多边形的有关计算化为一个边长分别是正多边形的半径、正多边形边长的一半,正多边形的边心距的直角三角形来解决.
5、正多边形的对称性
①多边形都是轴对称图形,当边数为偶数时,它的对称轴是每一边的垂直平分线和正多边形的边心距所在的直线,当边数为奇数时,它的对称轴是边心距所在的直线;
②只有正偶边形才是中心对称图形;
③正n边形绕着它的中心每旋转
就与它本身重合.
典例讲解
例1、填空题
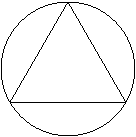
1. 如图,小颖同学在手工制作中,把一个边长为12cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则该圆的半径为( )
A.
B.
C.
D.
答案:D
2. 正六边形两条平行边间的距离是1,则它的边长为( )
A.
B.
C.
D.
答案:C
3. 已知正三角形的边长为2,则它的内切圆和外接圆组成的圆环面积为( )
A.
B.
C.
D.
答案:B
4. 边长为a的正三角形的边心距、半径和高之比为( )
A.1∶2∶3 B.
C.
D.
答案:A
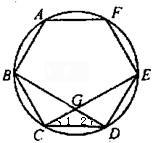
例2、如图,圆内接正六边形ABCDEF中,对角线BD、EC相交于点G,求∠BGC的度数.
解:
正六边形ABCDEF中DC=DE,
,
∴
,
同理可证:∠2=
,∴∠BGC=∠1+∠2=
.
例3、如图,已知正三角形ABC外接圆的半径为R,求正三角形ABC的边长、边心距、周长和面积.
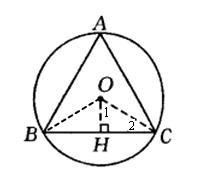
思路点拨:
过中心向正多边形的边作垂线得到Rt△OCH,在Rt△OCH中包含了中心角的一半、边心距、半径、边长的一半等基本元素.
解:
连接OB、OC,作OH⊥BC于H.
例4、如图,正方形的边长为4cm,剪去四个角后成为一个正八边形,求这个正八边形的边长和面积.

解:
由题意知PD=PE=FQ
设PD=PE=FQ=xcm,则EF=ED=(4-2x)cm,
∵∠P=90°,由勾股定理ED=
,
∴
,
∴正八边形的边长为4-2x=
cm,
面积为
.
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -