| 概率 |
主编:黄冈中学数学集体备课组
知识点归纳
1.确定事件
(1)必然事件
在一定条件下,一定能发生的事件,或者说发生的可能性是100%的事件,称为必然事件.
(2)不可能事件
在一定条件下,一定不能发生的事件,称为不可能事件.
2.不确定事件
(1)随机事件:
在一定条件下,可能发生也可能不发生的事件,称为随机事件.
(2)随机事件的大小
一般的,随机事件发生的可能性是有大小的,不同的随机事件发生的可能性的大小有可能不同.
3.概率的意义
对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A发生的概率. 记作P(A).
4.概率的计算公式
如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m个结果,那么事件A发生的概率P(A)=
指出:(1)这个概率的计算公式具有两个特点,即每一次试验中,可能出现的结果只有有限个;每一次试验中,各种结果出现的可能性相等.
(2)当A为必然事件时,P(A)=1;
(3)当A为不可能事件时,P(A)=0;
(4)事件A发生的可能性越大,P(A)越接近1,但P(A)≠1;
(5)事件A发生的可能性越小,P(A)越接近0,但P(A)≠0.
典例讲解
例1、填空题
1.按下面的要求,分别举出一个生活中的例子:
①随机事件________________;
②不可能事件________________;
③必然事件________________.
2.向上同时抛掷10枚硬币,出现10枚硬币均正面朝上的事件是__________ (填“确定事件”或“不确定事件”).
3.一个盒子中装有形状和大小完全相同的9个小球,其中5个黑球、2个红球、2个白球,现从中一次摸出三个球,则一定有黑色的球,这个事件是___________ (填“确定事件”或“不确定事件”).
4.袋中装有10个红球、5个白球,则在看不到球的情况下,随机从袋中摸出一球,摸到_________的可能性大一些.
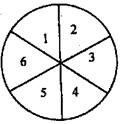
5.在如图所示的转盘中,指针落在_________区域的可能性大.

6.抛掷一枚硬币,正面朝上的概率为50%的意思是说____________.
7.一种彩票的中奖概率是
,其意思是_______________.
答案:
1、①2010年9月6日是晴天;②太阳从西边升起;③太阳每天早上从东方升起.
2、不确定事件
3、不确定事件
4、红球
5、红色
6、抛掷若干次硬币,平均每两次有一次正面朝上
7、购买(发行)若干张彩票,平均每1000张中有一张中奖
例2、选择题
1.下列事件中,属不确定事件的是( )
A.海口市的年平均气温比哈尔滨市的年平均气温高
B.从装有10个黄球,4个白球的袋中,随机取出2个球.其中一个黄球、一个白球.
C.每晚7点,中央电视台1套播出“新闻联播”节目
D.从装有50个黄球的袋中随机取出2个小球,这两个球都是白色的
2.下列事件是必然事件的是( )
A.抛掷一枚硬币,正面向上
B.掷一枚骰子,出现偶数点朝上
C.守株待兔
D.对于任意有理数x,有x2+1>0
3.下列事件中属于必然事件的是( )
A.明天我市下雨
B.太阳从西边升起
C.一口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球
D.我走出校门,看到的第一辆汽车的牌照的末位数字是偶数
4.在一场体育比赛前,教练预测“根据我掌握的情况,这场比赛,我们队有60%的机会获胜,”与“60%机会获胜”意思最接近的是( )
A.他这个队赢的可能性较大
B.若这两个队打10场比赛,他这个队会赢6场左右
C.若这两个队打100场比赛,他这个队恰好会赢60场
D.若这两个队打100场比赛,他这个队会赢60场左右
5.掷一个均匀的正四面体骰子,骰子每个面分别标有数字1、2、3、4,则2朝下的概率与4朝下的概率( )
A.P(4)>P(2) B.P(4)<P(2)
C.P(4)=P(2) D.不确定
6.如图所示:转盘被划分成六个相同大小的扇形,并分别标上1、2、3、4、5、6这6个数字,指针停在每个扇形区域的可能性相同,四位同学各自发表了下述见解:
甲:如果指针前三次都停在3号扇形,下次就一定不会停在3号扇形
乙:只要连续转6次,一定会有一次停在6号扇形
丙:指针停在奇数号扇形的概率与停在偶数号扇形的概率相等
丁:运气好的时候,只要在转动前默默想好,让指针停在6号扇形,
则停在6号扇形的可能性会加大.
其中,你认为正确的意见有( )
A.1个 B.2个 C.3个 D.4个
答案:
1、B 2、D 3、C 4、D 5、C 6、A
例3、在一个不透明的口袋中装有大小、外形完全相同的6个红球、4个蓝球、1个黄球,在不看球的情况下,从袋中摸出一个球,问:
(1)这个球可能是什么颜色?
(2)这个球可能是黑球吗?
(3)这个球可能是红球吗?
(4)如果再从袋中取出一个球,则这两个球的颜色可能相同吗?
解:
(1)可能是红或蓝或黄球;(2)不可能;(3)可能;(4)若第一个球是红色、蓝色,可能;若第一个球是黄色,不可能.
例4、不透明纸袋中有若干个除颜色外完全相同的黑色与白色小球,从中随机摸取一个球是白球的概率为
,若再放入7个白球,则摸到白球的概率为
,求原来袋中有多少个白球,多少个黑球?
解:
设原来袋中有x个白球,y个黑球,则
,∴
故原来袋中有8个白球,10个黑球.
例5、掷一枚骰子,求下列事件的概率:
(1)朝上的点数为1或6;
(2)朝上的点数是2的倍数和3的倍数.
解:
掷一枚骰子,朝上的点数可能为1,2,3,4,5,6共6种,这些点数出现的可能性相等;
(1) 朝上的点数为1或6的结果有2个,
故P(点数为1或6)=
(2) 朝上的点数是2的倍数和3的倍数的结果有4个,
故P(点数是2的倍数或3的倍数)=
.
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -