例1、已知x、y都为正整数，且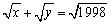
．求x＋y 的值．
思路：
因为只有化简后被开方数相同的二次根式才能合并，而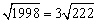
，易知
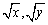化简后的被开方数必为222，故可设
．由此求出正整数a、b即可求出x、y．
解：
，（a，b为正整数），于是
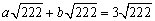即a＋b=3
∴a=2，b=1或a=1，b=2．
故x=222，y=888或x=888，y=222，
∴x＋y=1110．
总结：
几个二次根式化简后被开方数相同，则它们可以合并，本题则是逆用该结论，即几个二次根式能合并成一个二次根式，则它们化简后的被开方数必相同．
例2、若a＝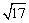
－1，求(a5＋2a4－17a3－a2＋18a－17)99的值．
思路：
本题若将a=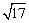
－1代入，确实繁杂，联想到以前学过的整体求值，因此应在a=
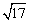－1上做文章．
解：
∵a=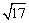
－1，∴(a＋1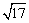)2=(
)2
即a2＋2a＋1=17．
又∵a5＋2a4－17a3－a2＋18a－17
= a5＋2a4－(a2＋2a＋1)·a3－a2＋(a2＋2a＋1＋1)a－(a2＋2a＋1)
=a5＋2a4－a5－2a4－a3－a2＋a3＋2a2＋2a－a2－2a－1
=－1．
∴原式=－1．
总结：
本题是构造出值为17的代数式，然后依据待求式中多次出现17的特点，采用宾主置换的方法，得到简捷的解法，也可以用降次的方法，即将a2＝16－2a代入降次求解．
