例1、阅读下面的例题及解答过程.
例:若方程x2-6x-k-1=0与x2-kx-7=0有相同根,试求k的值和相同根.
解:
设相同根为a,则它同时满足上述两方程
即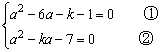
所以a2-6a-k-1=a2-ka-7,
即(6-k)a=6-k,
当k≠6时,a=1,把a=1代入②中,得k=-6;
当k=6时,代入原方程中,两方程均为x2-6x-7=0.
解得x1=-1,x2=7.
故当k≠6时,有一个相同根是x=1;当k=6时,它们的两个相同根是-1和7.
依照上述解题过程,解答下列问题:
已知k为非负实数,当k取什么值时,关于x的方程x2+kx-1=0与x2+x+k-2=0有相同的实根?
解:
设相同根为a,则

∴a2+ka-1=a2+a+k-2,
(k-1)a=k-1.
当k-1≠0时,a=1,把a=1代入①中,得k=0,此时x=±1;
当k-1=0时,即k=1时,代入原方程中,两方程均为
x2+x-1=0,

∴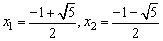 .
.
故当k≠1时,有两相同根是1和-1;
当k=1时,它们的两个相同根为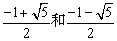 .
.
例2、已知12<m<60,且关于x的二次方程x2-2(m+1)x+m2=0有两个整数根,求整数m,并求此两个整数根.
解:
根据求根公式有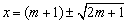
∵x1,x2都是整数,
∴2m+1必是完全平方数,
由于12<m<60,则25<2m+1<121.
∵m为整数,∴2m+1是奇数
∴只能是2m+1=72或2m+1=92
解之得m1=24,m2=40
当m=24时,x1=32,x2=18;
m=40时,x1=50,x2=32.