解方程：（x2－2x）2＋（x2－2x）－2＝0
分析：
把x2－2x当成一个整体，用y来代换，原方程可变为：y2＋y－2＝0，用因式分解法解这个方程（y＋2）（y－1）＝0，得y＝－2或y＝1，再解关于x的方程x2－2x＝－2和x2－2x＝1．
解：
设y＝x2－2x
原方程可变为：y2＋y－2＝0
得（y＋2）（y－1）＝0，
所以y＋2＝0或y－1＝0
得y＝－2或1，所以x2－2x＝－2或1．
当x2－2x＝－2时，△＜0，无实数根，
当x2－2x＝1时，解得x＝1±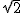
．
∴原方程的根是x1＝1＋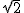
，x2＝1－
．
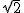