例1、质量为2kg的物体在水平推力F的作用下沿水平面作直线运动,一段时间后撤去F,其运动的v-t图像如图所示。g取10m/s2,求:

(1)物体与水平面间的运动摩擦系数μ;
(2)水平推力 的大小;
的大小;
(3)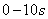 内物体运动位移的大小。
内物体运动位移的大小。
答案:
(1)0.2 (2)6N (3)46m
解析:
(1)设物体做匀减速运动的时间为Δt2、初速度为v20、末速度为v2t、加速度为a2,则
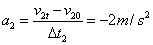 ①
①
设物体所受的摩擦力为Ff,根据牛顿第二定律有
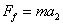 ②
②
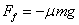 ③
③
联立②③得: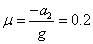 ④
④
(2)设物体做匀减速运动的时间为Δt1、初速度为v10、末速度为v1t、加速度为a1,则
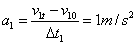 ⑤
⑤
根据牛顿第二定律有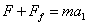 ⑥
⑥
联立③⑥得: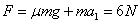
(3)解法一:由匀变速运动的位移公式得:
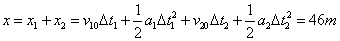
解法二:根据v-t图像围成的面积得:
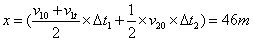
例2、质量为M的拖拉机拉着耙来耙地,由静止开始做匀加速直线运动,在时间t内前进的距离为s。耙地时,拖拉机受到的牵引力恒为F,受到地面的阻力为自重的k倍,把所受阻力恒定,连接杆质量不计且与水平面的夹角θ保持不变。求:

(1)拖拉机的加速度大小。
(2)拖拉机对连接杆的拉力大小。
(3)时间t内拖拉机对耙做的功。
答案:
(1)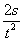
(2)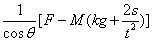
(3)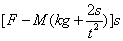
解析:
(1)拖拉机在时间t内匀加速前进s,根据位移公式
 ①
①
变形得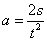 ②
②
(2)对拖拉机受到牵引力、支持力、重力、地面阻力和连杆拉力T,根据牛顿第二定律
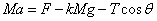 ③
③
联立②③变形得 ④
④
根据牛顿第三定律连杆对耙的反作用力为
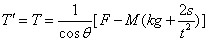 ⑤
⑤
拖拉机对耙做的功: ⑥
⑥
联立④⑤解得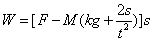 ⑦
⑦