| 牛顿运动定律瞬时性问题和正交分解法 |
主编:黄冈中学物理集体备课组
a.对于两端均有约束的轻弹簧或橡皮条,若两端约束均未消除,则该一瞬间形变量来不及变化,弹力不变.若有一端解除约束,轻弹簧或橡皮条弹力突变为0.
b.对钢性杆,不可伸长的轻绳上的力可以发生突变.
例1、如图示,球A、B、C质量分别为m、2m、3m,A与天花板间、B与C之间用轻弹簧相连,当该系统平衡后,突然将AB间轻绳绕断,在绕断瞬间,A、B、C的加速度(以向下为正方向)分别为( )
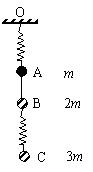
A.0、g、g B.-5g、2.5g、0
C.5g、2.5g、0 D.-g、2g、2g
解:
在A、B间轻绳烧断前,A、B、C均处于平衡状态,即:
当A、B间轻绳烧断瞬间:
各弹簧的形变量还来不及变化,故在轻绳烧断瞬间,弹簧的弹力在这一瞬间未变化:
A.
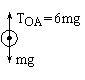
方向竖直向上
B.
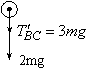
方向竖直向下
C.
aC=0
例2、提问:两质量均为m的小球,A图中通过不可伸长的轻绳相连,A、B图中两种情况开始用手拿着顶端的小球,突然释放瞬间.问A、B两种情况下,两球在这一瞬间的加速度.
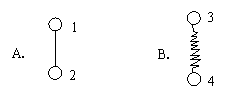
松手瞬间发生突变:a1=a2=g a3=2g,a4=0
例3、如图所示,两根细线OA、OB共同拉住一个质量为m的小球,平衡时OB细线是水平的,OA细线与竖直方向夹角为θ,若剪断水平细线OB的瞬间,OA线的拉力大小是___________,小球加速度的大小为___________,方向与竖直方向的夹角大小等于___________.
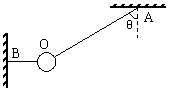
解:因绳子不能伸长,沿绳方向合力为零,剪断OB瞬间,OA绳拉力发生突变:
①剪断OB绳时:沿OA绳合力为零(绳不可伸长)
球所受合力沿绳切线方向mgsinθ=ma1
a1=gsinθ 方向垂直OA绳向下
此时TOA=mgcosθ
推广:②若剪断OA绳时:a′=g 方向竖直向下 TOB=0
如图所示,一根轻弹簧和一根细线共同拉住一个质量为m的小球,平衡时细线是水平的.弹簧与竖直方向夹角为θ,剪断细线的瞬间,弹簧的拉力大小是___________,小球加速度的大小为___________,方向与竖直方向夹角大小等于___________.
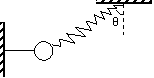
解:
①剪断细线瞬间,弹簧两端约束还未解除,弹簧弹力来不及变化.
T弹=mg/cosθ F合=mgtanθ a=gtanθ 方向水平向右
②若剪断弹簧 a′=g 竖直向下
例4、mA∶mB∶mc=1∶2∶3,求绳断瞬时:
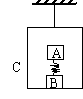
aA=? aB=? aC=?
答案:aA=0 aB=aC=1.2g
二、力的正交分解:
在物体受多个力作用时,常把各力都分解在两个互相垂直的方向(通常把这两个方向分别称为x轴和y轴,但这并不一定是水平和竖直方向),然后分别求每个方向上的力的代数和。满足
这样就可把复杂的矢量运算转化为互相垂直方向上的简单的代数运算。
例5、质量为m的人站在自动扶梯上,扶梯正以加速度a向上加速运动,a与水平方向的夹角为θ,则人所受的支持力大小为________,摩擦力大小为________,方向为________。
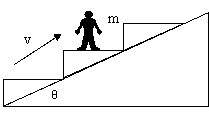
ax=acosθ
ay=asinθ
由牛顿第二定律得
Ff=max
FN-mg=may
求得Ff=macosθ,方向水平向右FN=m(g+asinθ)
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -