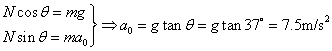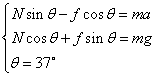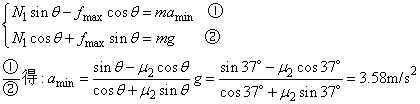| 牛顿第二定律解决临界状态的问题 |
主编:黄冈中学物理集体备课组
当物体的运动状态变化时,一些相关的物理量也会随之发生变化,在动力学问题中出现的“最大”、“最小”、“刚好”、“恰能”等词暗示了临界状态的出现,隐含着相应的临界条件,在动力学中常见的临界问题主要是由于弹力、摩擦力是被动力,弹力、摩擦力发生突变就是临界状态.
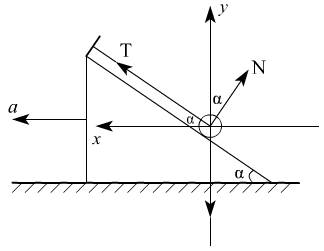
例1、如图所示,将质量为10kg的小球挂在倾角α=45°的光滑斜面上.
(1)当斜面以加速度
沿图示方向运动时,求绳中的张力.
(2)当斜面以加速度
沿图示方向运动时,求绳中的张力.
解:
小球在斜面上,当N=0时:
Tcosα=ma0 ①
Tsinα=mg ②
由①②得:a0=gcotα=g
(1)当
<a0=g时:小球未离开斜面,且斜面对小球有支持力N:
Tcosα-Nsinα=ma ③
Tsinα+Ncosα=mg ④
③×cosα+④×sinα,则T=mgsinα+macosα=0.94mg,
④×cosα-③×sinα,则N=mgcosα-masinα=
=0.47mg.
(2)当
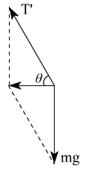
>a0=g时,小球离开斜面,设此时轻绳与水平方向夹角为θ
T′cosθ=ma2 ⑤
T′sinθ=mg ⑥
T′=
=2mg,θ=30°,说明绳与水平方向夹角为30°.
分析:
保证m、M一起向左匀加速直线运动.
若F过大,则m和M一起加速度过大,N和mg的合力不足以提供加速度,斜面对m施加沿斜面向下的摩擦力f.
若F过小,则m和M一起加速度过小,N和mg的合力提供加速度还有余,则斜面对m施加的摩擦力沿斜面向上.
当f=0时,a=a0,则a>a0,f沿斜面向下.a<a0,f沿斜面向上.
例2、水平地面上,放置倾角θ=37°三角形滑块,M=3kg,斜面上放置质量m=1.0kg的物块,三角形滑块与地面间动摩擦因数μ1=0.25.当用F=30N的水平力推三角形滑块时,物块与m一起加速运动,且没有相对滑动.求:(g=10m/s2)
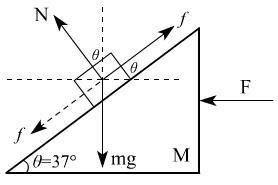
(1)物块m所受摩擦力的大小和方向;
(2)若物块m与斜面间的动摩擦因数μ2=0.3,要使m与M之间不发生相对滑动,求水平力F的大小.
解:
(1)当f=0时:
对m、M作为一个整体,则:
F-μ1(M+m)g=(m+M)a
因a<a0,故M对m的f沿斜面向上.
解得f=2N,沿斜面向上.
(2)当Fmin,使m和M一起运动,具有水平向左的最小加速度,此时刚好m相对M恰好要下滑而未下滑,m受到沿斜面向上的fmax.
N1=10.2N
∴Fmin-μ1(m+M)g=(M+m)amin
Fmin=μ1(m+M)g+(M+m)amin=24.3N
当Fmax时,使m和M一起匀加速运动,具有水平向左的最大加速度,此时刚好m相对M恰好要上滑而未上滑,m受到沿斜面向下的fmax.
Fmax-μ1(M+m)g=(M+m)amax
Fmax=μ1(M+m)g+(M+m)amax=63.6N
∴保证m在M上不发生相对滑动,则24.3N≤F≤63.6N.
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -