| 有关传送带上的牛顿第二定律的应用问题 |
主编:黄冈中学物理集体备课组
知识点:应用牛顿第二定律
,所求a均是物体对地的运动.
例1、传送带A、B两轮L=6m,皮带匀速v=3m/s向右传动,m=1kg物体无初速放在皮带一端A点,μ=0.2.求物体从A运动至B所需时间?
解:
物体在皮带上运动过程分为两个阶段:
(1)第一阶段:物体无初速放上皮带对地作初速为0,a=μg匀加速运动,位移s1、时间t1.
对地位移s1=
=2.25m
(2)第二阶段:物体与皮带以共同速度向右匀速运动.
至B对地位移s2=L-s1=6-2.25m=3.75m
匀速运动时间t2=
=1.25s
则物体从A→B时间t=t1+t2=2.75s
小结:
1、不管皮带作什么运动,物体相对地面的位移从A→B即离开皮带.
2、物体轻轻地放上皮带,相对皮带向左运动,但相对地面向右作初速为0的匀加速直线运动,直到速度增加到皮带相等速度,与后皮带一起作匀速直线运动.
例2、传送带L=8m,物体m=10kg以v0=10m/s水平滑上传送带,物体与传送带μ=0.6,物体可视为质点,g=10m/s2.求:
(1)若传送带静止,物体从传送带左端A滑到右端B所需时间;
(2)若传送带以速度v=4m/s沿顺时针方向匀速转动,物体从A→B所需时间;
(3)若传送带以速度v=4m/s逆时针方向匀速转动,物体是否能从传送带A端滑至B端?如不能说明理由.如能,计算所经历时间.
解:
(1)当传送带静止时,物体在传送带上作初速v0=10m/s,a=μg=6m/s2做匀减速直线运动.当物体速度减为0历时
.速度减为0过程对地位移
,
∴物体在速度减为0之前已从A滑至B点,
s=v0t-
8=10t-
×6t2
t1=2s或t2=
讨论:t=2s是物体A→B继续向前匀减速至速度为0后反向匀加速至B点,故t=2s舍,t=
.
(2)若传送带以v=4m/s顺时针方向匀速转动:
物体先相对地作初速v0=10m/s,a=μg=6m/s2对地匀减速直线运动至传送带速度,历时t1,对地位移s1
然后物体相对传送带静止一起匀速运动,对地位移s2=L-s1=1m
历时
∴t总=t1+t2=1.25s.
(3)若传送带以速度v=4m/s沿逆时针方向匀速转动,物体相对地面作初速为v0=10m/s,加速度大小为a=μg=6m/s2的匀减速直线运动,不管皮带怎样运动,传送带相对地面位移为s=|AB|,即A→B.s=v0t-
8=10t-
×6t2
t1=2s(舍)t2=
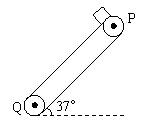
例3、传送带全长LAB=16m,且与水平方向成37°夹角,并以10m/s的速度匀速运动,现将质量为m的小物块(可视为质点)轻轻地放在传送带上的P点处,如图所示.已知小物块与传送带间的动摩擦因数μ=0.5,则小物块从传送带上的P点运动到Q点所用时间可能是__________.
解:
(1)当传送带顺时针转动时,物块所受滑动摩擦力方向向上,其加速度
小物块相对地面作初速为0的匀加速直线运动,
从P→Q运动时间为t:
(2)当传送带逆时针转动,小物块无初速地释放在P点,物块所受滑动摩擦力方向向下,加速度为:
经时间t1小物块对地作匀加速直线运动至速度达与传送带相同速度,对地滑行距离s1,则:
之后,由于μ<tanθ,物体所受重力沿斜面方向的分量大于最大静摩擦力,物块所受滑动摩擦力向上,加速度为a2,
物块位移为s2=s-s1=(16-5)m=11m
∴由s2=vt2+
11=10t2+
得:t2=1s或-11(舍)
∴t总=t1+t2=2s.
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -