1、如图所示,一水平传送带以v=2 m/s的速度做匀速运动,将一物体轻放在传送带一端,已知物体与传送带间的动摩擦因数为0.1,物体由传送带一端运动到另一端所需时间为11 s,求传送带两端的距离.(g取10 m/s2)
显示答案
解析:物体在刚放上传送带的瞬间,物体的速度为零,而传送带有速度,物体被加速,滑动摩擦力是物体所受的合外力,由牛顿第二定律,得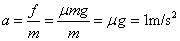 ,经时间 ,经时间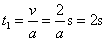 后,物体与传送带同速,此后物体做匀速直线运动,共9s. 后,物体与传送带同速,此后物体做匀速直线运动,共9s.
匀加速位移x1=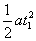 =2 m,匀逮运动的位移x2=v·t2=18 m,所以物体的总位移x=x1+x2=20m,即传送带两端的距离. =2 m,匀逮运动的位移x2=v·t2=18 m,所以物体的总位移x=x1+x2=20m,即传送带两端的距离.
答案:20m |
2、如图所示,绷紧的传送带与水平面的夹角θ=30°,皮带在电动机的带动下,始终保持以v0=2m/s的速率运行.现把一质量为m=10kg的工件(可视为质点)轻轻地放在皮带的底端,经时间1.9s,工件被传送到h=1.5m的高处,g取10m/s2.求工件与皮带间的动摩擦因数.
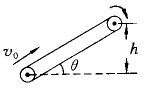
显示答案
解析:设工件上升1.5 m的过程中,加速运动的时间为t1,匀速运动的时间为t-t1,
则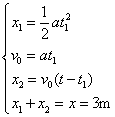
联立以上几式解得a=2.5 m/s2.
由牛顿第二定律得mgcos 30°-mgsin 30°=ma,解得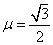 . .
答案: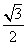 |
3、如图所示,一辆质量为M的卡车沿平直公路行驶,卡车上载一质量为m的货箱,货箱到车前部的距离l已知,货箱与底板的动摩擦因数为μ,当卡车以速度为v0行驶时,因前方出现故障而制动,制动后货箱在车上恰好滑行了距离l而未与卡车碰撞,求:
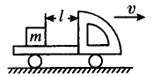
(1)卡车制动的时间;
(2)卡车制动时受地面的阻力.
显示答案
解析:(1)设卡车制动的时间为t,则卡车制动过程中通过的位移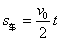 . .
货箱向前滑动受摩擦力产生的加速度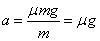
货箱运动时间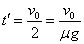
货箱位移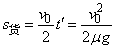
又因制动过程中车对地位移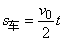
则有s货=s车+l,即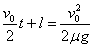
解得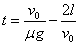
(2)设卡车制动时受地面阻力为F地,卡车制动加速度为a车,由牛顿第二定律得
F地-μmg=Ma车 ①
又因v0=a车t ②
联系①②解得
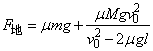
本题还可以结合v-t图象求解,如图所示.
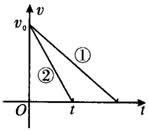
其中②为车制动的v-t图象,①是货箱运动的v-t图象,其位移之差即为l.
由图象可得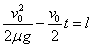
可得
由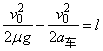 ,F地-μmg=Ma车 ,F地-μmg=Ma车
可得 |
4、如图所示,传送带与水平面的夹角为37°,以v=10m/s的速度匀速运动,在传送带的A端轻轻放一小物体,已知物体与传送带间的动摩擦因数μ=0.5,AB间距离s=16m(g=10m/s2,cos37°=0.8,sin37°=0.6).则:
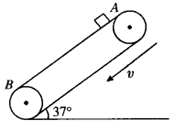
(1)若转动方向为顺时针方向,小物体从A端运动到B端所需要的时间为( )
A.2.8s B.2.0s C.2.1s D.4.0s
(2)在(1)的选项中,若皮带逆时针转动,小物体从A端运动到B端所需要的时间为( )
A.2.8s B.2.0s C.2.1s D.4.0s
显示答案
解析:(1)对物体受力分析如图所示,沿皮带所在斜面方向a=gsin37°-μgcos37°=2m/s2.

a沿皮带向下,物体与皮带运动方向相反.所以整个过程物体对地匀加速运动16m,据s=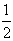 at2得t=4.0s. at2得t=4.0s.
(2)此运动分为两个阶段.
第一阶段:物体加速至与皮带共速,刚放上物体时.皮带受摩擦力向上,而物体受摩擦力向下,如图所示,物体以加速度a1=gsin37°+μgcos37°=10m/s2,匀加速运动,经过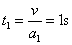 与皮带达共同速度.对应位移s= 与皮带达共同速度.对应位移s= =5m. =5m.
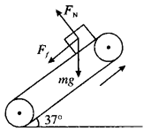
第二阶段:共速以后,物体沿皮带速度大于皮带的速度,物体相对皮带下滑,受摩擦力变向,如(1)问解析图所示,a2=gsin37°-μgcos37°=2m/s2,方向向下,使物体继续加速.则
(16-5)=10t2+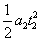 , ,
解得t2=1s,从A到B共需t=t1+t2=2s,选B.
答案:(1)D (2)B |
5、一水平的浅色长传送带上放置一煤块(可视为质点),煤块与传送带之间的动摩擦因数为μ.初始时,传送带与煤块都是静止的.现让传送带以恒定的加速度a0开始运动,当其速度达到v0后,便以此速度做匀速运动.经过一段时间,煤块在传送带上留下了一段黑色痕迹后,煤块相对于传送带不再滑动.求此黑色痕迹的长度.
显示答案
解析:根据“传送带上有黑色痕迹”可知,煤块与传送带之间发生了相对滑动,煤块的加速度a小于传送带的加速度a0.根据牛顿定律,可得a=μg.
设经历时间t,传送带由静止开始加速到速度等于v0,煤块则由静止加速到v,有v0=a0t,v=at.
由于a<a0,故v<v0,煤块继续受到滑动摩擦力的作用.再经过时间t′,煤块的速度由v增加到v0,有v0=v+at′.
此后,煤块与传送带运动速度相同,相对于传送带不再滑动,不再产生新的痕迹.
设在煤块的速度从0增加到v0的整个过程中,传送带和煤块移动的距离分别为s0和s.有
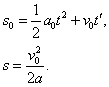
传送带上留下的黑色痕迹的长度l=s0-s.
由以上各式得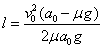 . . |
6、如图9所示,一平直的传送带以速度v=2m/s匀速运动,传送带把A处的工件运送到B处,A、B相距L=10m.从A处把工件无初速地放到传送带上,经过时间为6s,能传送到B处.欲用最短的时间把工件从A处传送到B处,求传送带的运行速度至少多大.

显示答案
解析:因为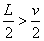 ,所以工件在6s内先匀加速运动,后匀速运动,有x1= ,所以工件在6s内先匀加速运动,后匀速运动,有x1=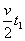 ,x2=vt2,t1+t2=t,x1+x2=L. ,x2=vt2,t1+t2=t,x1+x2=L.
解上述四式得t1=2s,a=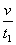 =1m/s2. =1m/s2.
若要工件以最短时间传送到B,工件先加速度仍为a,设传送带速度为v,工件先加速后匀速,同上有L=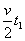 +vt2. +vt2.
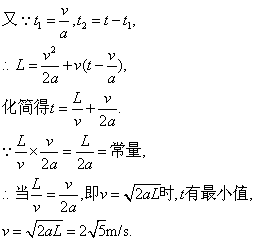
表明工件一直加速到B所用时间最短.
|
7、如图水平传送带的长度为L=8m,A、B为传送带水平部分的最左端和最右端.现有一物体(视为质点)以v0=10 m/s的初速度从A端水平地滑上水平传送带.已知物体与传送带之间的动摩擦因数为μ=0.6,g取10 m/s2.试求:

(1)若传送带保持静止,物体滑到B端时,物体的速度为多大?
(2)若皮带轮逆时针匀速转动,传送带转动的速率恒为8 m/s,则物体到达B端时的速度是多大?
(3)若皮带轮顺时针匀速转动,传送带转动的速率恒为8 m/s,则物体从A端到达B端所用的时间是多少?
显示答案
解析:(1)由a=-μg,2ax=vB2-v02,代入数据解得到达B端时物体的速度为:vB=2 m/s
(2)若皮带轮逆时针匀速转动,物体的受力及运动情况与传送带静止时完全相同,故到达B端时其速度也是2m/s.
(3)令物体速度从v0=10 m/s减速到v1=8m/s所需的时间为t1,则由v1=v0+at1,代入数据得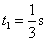 . .
由2ax1=v12-v02,代入数据得x1=3m.
故x1<L,故物体先匀减速后匀速运动.
设匀速运动过程所需时间为t2,则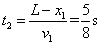 . .
故物体从A端到达B端所用的总时间是:t总=t1+t2=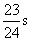 =0.958s. =0.958s.
答案:(1)2 m/s (2)2 m/s (3)0.958s |
|